PROVING STATEMENTS ABOUT SEGMENTS
About "Proving statements about segments"
Proving statements about segments :
A true statement that follows as a result of other statements is called a theorem. All theorems must be proved. We can prove a theorem using a two-column proof. A two-column proof has numbered statements and reasons that show the logical order of an argument.
Theorem : Properties of Segment Congruence
REFLEXIVE
SYMMETRIC
TRANSITIVE
For any segment AB, AB ≅ AB
If AB ≅ CD, then CD ≅ AB
If AB ≅ CD, and CD ≅ EF, then AB ≅ EF
A proof which is written in paragraph form is called as paragraph proof.
Here is a paragraph proof for the Symmetric Property of Segment Congruence.
Paragraph Proof :
We are given that PQ ≅ XY. By the definition of congruent segments, PQ = XY. By the symmetric property of equality, XY = PQ. Therefore, by the definition of congruent segments, it follows that XY ≅ PQ.
Proving statements about segments - Examples
Example 1 :
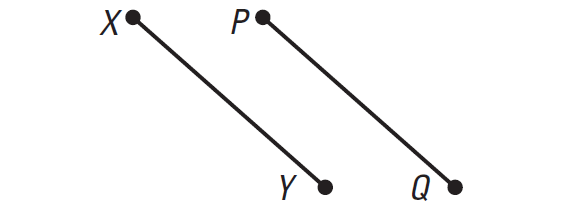
In the diagram given above, PQ ≅ XY. Prove XY ≅ PQ
Solution :
PQ ≅ XY
PQ = XY
XY = PQ
XY ≅ PQ
Given
Definition of congruence statements
Symmetric property of equality
Definition of congruence segments
Example 2 :
Use the diagram and the given information to complete the missing steps and reasons in the proof.
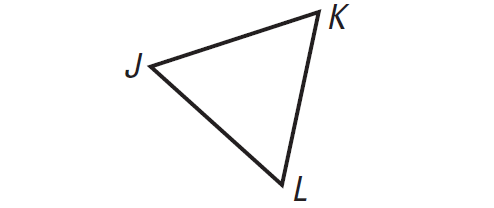
Given : LK = 5, JK = 5, JK ≅ JL
Prove : LK ≅ JL
A
B
LK = JK
LK ≅ JK
JK ≅ JL
D
Given
Given
Transitive property of equality
C
Given
Transitive property of congruence
Solution :
A. LK = 5
B. JK = 5
C. Definition of congruence segments
D. LK ≅ JL
Example 3 :
In the diagram given below, Q is the midpoint of PR.
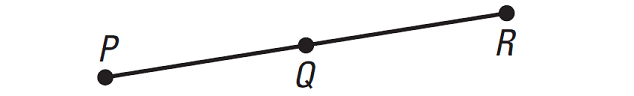
Show that PQ and QR are each equal to 1/2 ⋅ PR.
Solution :
Given : Q is the midpoint of PR
Prove : PQ = 1/2 ⋅ PR and QR = 1/2 ⋅ PR
Q is the midpoint of PR
Given
PQ = QR
PQ + QR = PR
PQ + PQ = PR
2 ⋅ PQ = PR
PQ = 1/2 ⋅ PR
QR = 1/2 ⋅ PR
Definition of midpoint
Segment Addition Postulate
Substitution property of equality
Distributive property
Division property of equality
Substitution property of equality
After having gone through the stuff given above, we hope that the students would have understood, how to prove statements about segments".
Apart from the stuff given above, if you want to know more about "Proving statements about segments", please click here
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
