PROVING STATEMENTS ABOUT SEGMENTS AND ANGLES

A true statement that follows as a result of other statements is called a theorem. All theorems must be proved. We can prove a theorem using a two-column proof. A two-column proof has numbered statements and reasons that show the logical order of an argument.

Theorem : Properties of Segment Congruence

Theorem : Properties of Angle Congruence

A proof which is written in paragraph form is called as paragraph proof.

Here is a paragraph proof for the Symmetric Property of Segment Congruence.

Paragraph Proof :

We are given that PQ ≅ XY. By the definition of congruent segments, PQ = XY. By the symmetric property of equality, XY = PQ. Therefore, by the definition of congruent segments, it follows that XY ≅ PQ.

Here is a paragraph proof for the Symmetric Property of Angle Congruence.

Paragraph Proof :

We are given that ∠A ≅ ∠B. By the definition of congruent angles, A = B. By the symmetric property of equality, B = A. Therefore, by the definition of congruent angles, it follows that ∠B ≅ ∠A.

Example 1 :

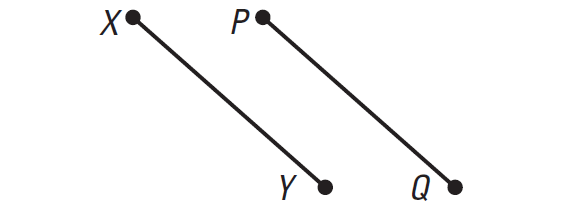
In the diagram given above, PQ ≅ XY. Prove XY ≅ PQ

Solution :

Example 2 :

Use the diagram and the given information to complete the missing steps and reasons in the proof.

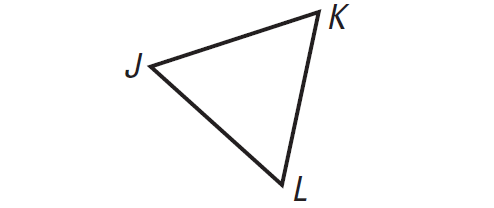
Given : LK = 5, JK = 5, JK ≅ JL

Prove : LK ≅ JL

Solution :

A.  LK  =  5

B.  JK  =  5

C.  Definition of congruence segments

D.  LK  ≅  JL

Example 3 :

In the diagram given below, Q is the midpoint of PR. 

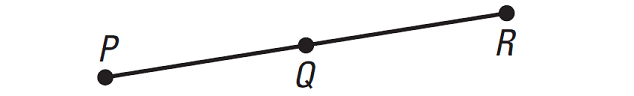
Show that PQ and QR are each equal to 1/2 ⋅ PR. 

Solution :

Given : Q is the midpoint of PR

Prove : PQ  =  1/2 ⋅ PR and QR  =  1/2 ⋅ PR

Example 4 :

Prove the Transitive Property of Congruence for angles.

Solution :

To prove the Transitive Property of Congruence for angles, begin by drawing three congruent angles. 

Label the vertices as A, B and C.

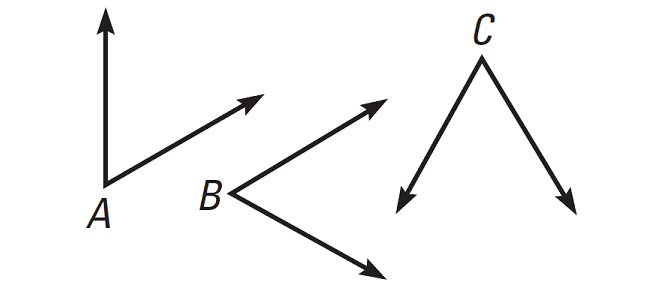
Given : 

∠A ≅ ∠B

∠B ≅ ∠C

Prove : 

∠A ≅ ∠C

Example 5 :

In the diagram shown below, 

m∠3 = 40°, ∠1 ≅ ∠2, ∠2 ≅ ∠3

Prove m∠1 = 40°

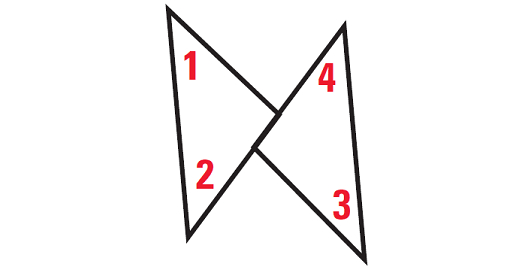
Solution :

Example 6 :

In the diagram shown below, 

∠1 and ∠2 are right angles

Prove ∠1 ≅ ∠2

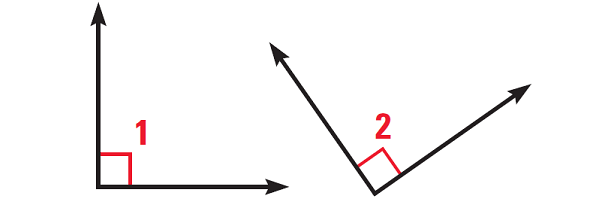
Solution :

Example 7 :

In the diagram shown below, 

∠1 and ∠2 are supplements,

∠3 and ∠4 are supplements,

∠1 ≅ ∠4

Prove ∠2 ≅ ∠3

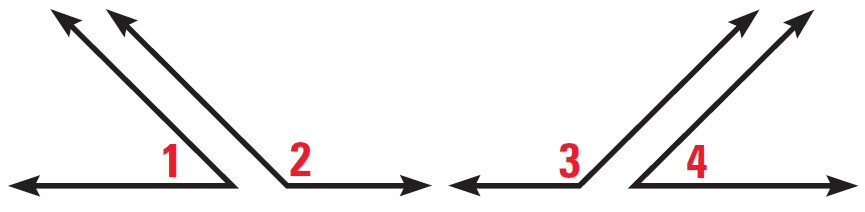
Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.