PROVING STATEMENTS ABOUT ANGLES WORKSHEET

Problem 1 :

Prove the Transitive Property of Congruence for angles.

Problem 2 :

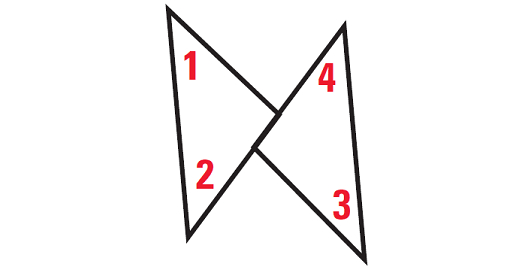
In the diagram shown below,

m∠3 = 40°, ∠1 ≅ ∠2, ∠2 ≅ ∠3

Prove m∠1 = 40°.

Problem 3 :

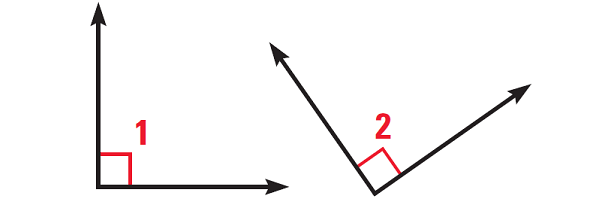
In the diagram shown below,

∠1 and ∠2 are right angles

Prove ∠1 ≅ ∠2

Problem 4 :

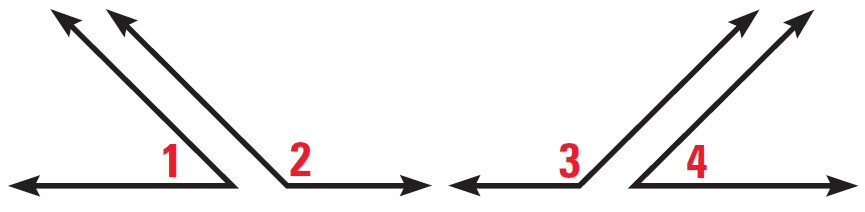
In the diagram shown below,

∠1 and ∠2 are supplements,

∠3 and ∠4 are supplements,

∠1 ≅ ∠4

Prove ∠2 ≅ ∠3

1. Answer :

To prove the Transitive Property of Congruence for angles, begin by drawing three congruent angles.

Label the vertices as A, B and C.

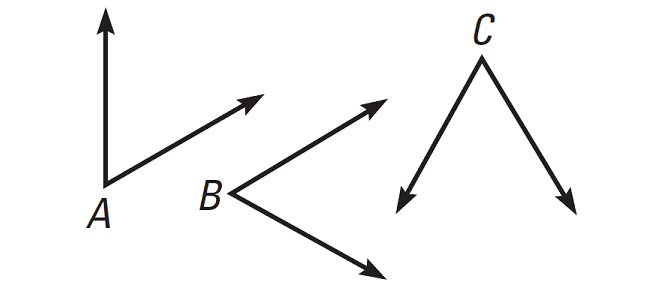
Given :

∠A ≅ ∠B

∠B ≅ ∠C

Prove :

∠A ≅ ∠C

Statements

∠A ≅ ∠B, ∠B ≅ ∠C

m∠A = m∠B

m∠B = m∠C

m∠A = m∠C

∠A ≅ ∠C

Reasons

Given

Definition of congruent angles

Transitive property of equality

Definition of congruent angles

2. Answer :

Statements

m∠3 = 40°

∠1 ≅ ∠2

∠2 ≅ ∠3

∠1 ≅ ∠3

m∠1 = m∠3

m∠1 = 40°

Reasons

Given

Transitive Property of Congruence

Definition of congruent angles

Substitution property of equality

3. Answer :

Statements

aaaa ∠1 and ∠2 are aa aaaaa right angles

m∠1 = 90°, m∠2 = 90°

m∠1 = m∠2

∠1 ≅ ∠2

Reasons

Given aaaaaaaaaaaaaaaaaaaaa aaaaaaaaa

Definition of right angle

Transitive property of equality

Definition of congruent angles

4. Answer :

Statements

∠1 and ∠2 are supplements

∠3 and ∠4 are supplements

∠1 ≅ ∠4

m∠1 + m∠2 = 180° m∠3 + m∠4 = 180°

m∠1 = m∠4

a ∠1 + ∠2 = ∠3 + ∠1 aaaaaa

m∠2 = m∠3

∠2 ≅ ∠3

Reasons

aaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaa

Given aaaaaaaaaaaaaaaaaaaaaa aaaaaa

Definition of Supplementary angles aaaaaaaaaaaaaaaaaaaa

Definition of congruent angles

Substitution property of equality aaaaaaaaaaaaaaaaaa

Subtraction property of equality

Definition of congruent angles

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

PROVING STATEMENTS ABOUT ANGLES WORKSHEET

Recent Articles

10 Hard SAT Math Questions (Part - 13)

10 Hard SAT Math Questions (Part - 12)

10 Hard SAT Math Questions (Part - 11)