PROVING QUADRILATERALS ARE PARALLELOGRAMS

In this section, you will learn how to prove that a quadrilateral is a parallelogram. 

We can use the following Theorems to prove the quadrilateral are parallelograms. 

Theorems

Theorem 1 :

If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

It has been illustrated in the diagram shown below.

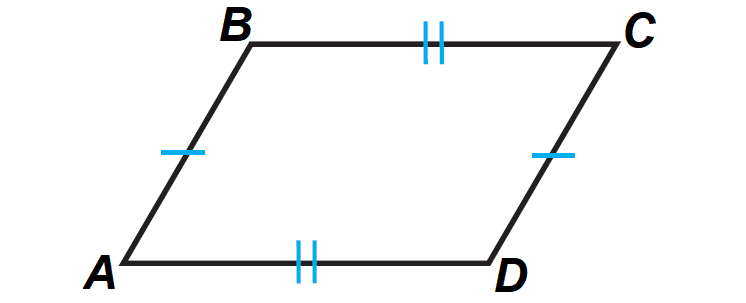
In the diagram above,

AB ≅ DC

AD ≅ BC

Theorem 2 :

If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

It has been illustrated in the diagram shown below.

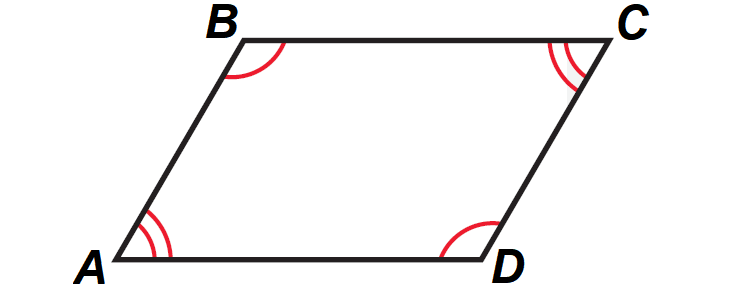
In the diagram above,

m∠A ≅ m∠C

m∠B ≅ m∠D

Theorem 3 :

If an angle of a quadrilateral is supplementary to both of its consecutive angles, then the quadrilateral is a parallelogram.

It has been illustrated in the diagram shown below.

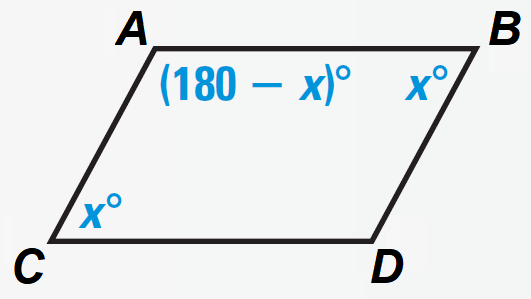
In the diagram above,

m∠A + m∠B = 180°

m∠B + m∠C = 180°

m∠C + m∠D = 180°

m∠A + m∠D = 180°

Theorem 4 :

If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.

It has been illustrated in the diagram shown below.

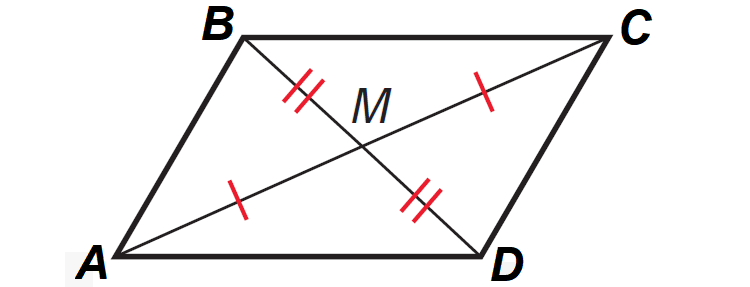
In the diagram above,

AM ≅ CM

BM ≅ DM

Theorem 5 :

If one pair of opposite sides of a quadrilateral are congruent and parallel, then the quadrilateral is a parallelogram.

It has been illustrated in the diagram shown below.

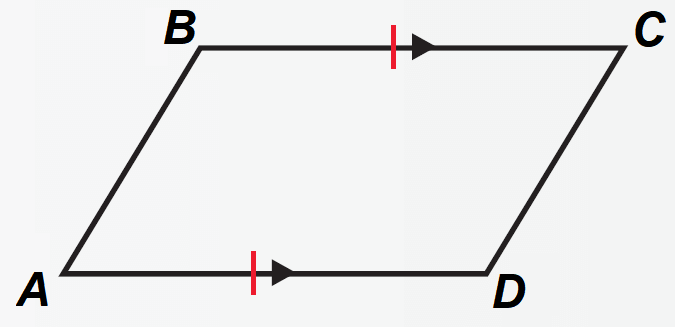
In the diagram above,

AD ≅ BC

AD || BC

Solved Problems

Problem 1 :

In the diagram given below, if AB ≅ CD, AD ≅ CB, then prove that ABCD is a parallelogram.

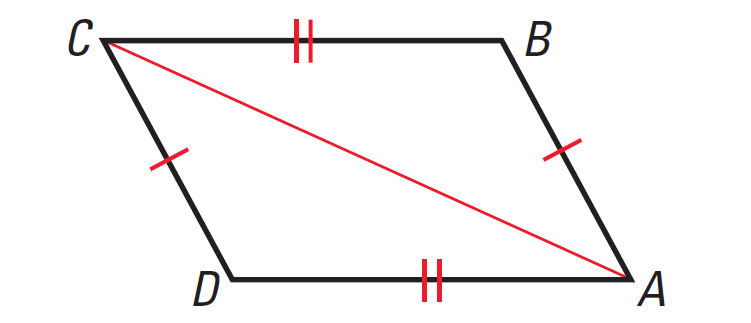
Solution :

Problem 2 :

In the diagram given below, if BC || DA, BC  ≅  DA, then prove that ABCD is a parallelogram.

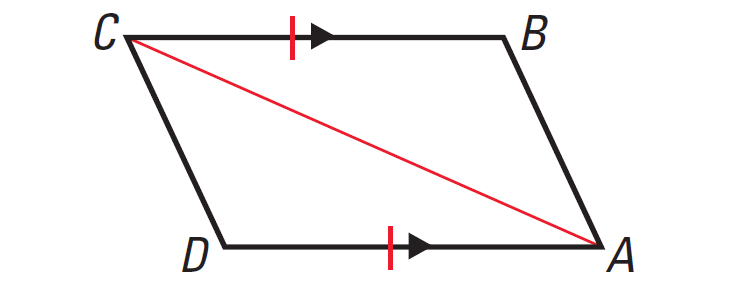
Solution :

Problem 3 :

Show that A(2, - 1), B(1, 3), C(6, 5) and D(7, 1) are the vertices of a parallelogram.

Solution :

Let us plot the given points in a coordinate plane as shown below.

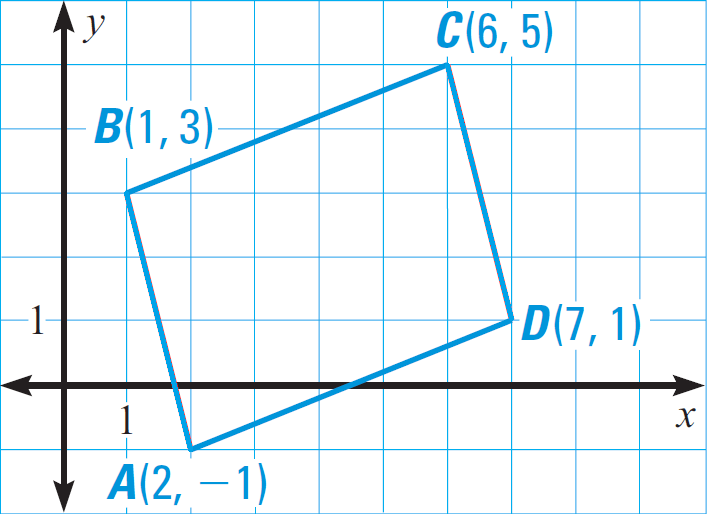
There are many ways to prove that the given points are the vertices of a parallelogram.

Method 1 :

Show that opposite sides have the same slope, so they are parallel.

Using slope formula to find the slopes of AB, CD, BC and DA.

Slope of AB = [3 - (-1)]/[1 - 2] = -4

Slope of CD = [1 - 5]/[7 - 6] = -4

Slope of BC = [5 - 3]/[6 - 1] = 2/5

Slope of DA = [- 1 - 1]/[2 - 7] = 2/5

AB and CD have the same slope. So they are parallel.

Similarly, BC and DA are parallel.

Because opposite sides are parallel, ABCD is a parallelogram.

Method 2 :

Show that opposite sides have the same length.

Using distance formula to find the lengths of AB, CD, BC and DA.

AB = √[(1 - 2)² + (3 + 1)²] = √17

CD = √[(7 - 6)² + (1 - 5)²] = √17

BC = √[(6 - 1)² + (5 - 3)²] = √29

DA = √[(2 - 7)² + (- 1 - 1)²] = √29

From the lengths AB, CD, BC and DA, it is clear that

AB ≅ CD and BC ≅ DA

Because both pairs of opposite sides are congruent, ABCD is a parallelogram.

Method 3 :

Show that one pair of opposite sides is congruent and parallel.

Find the slopes and lengths of AB and CD as shown in Methods 1 and 2.

Slope of AB = Slope of CD = -4

Because AB and CD have the same slope, they are parallel.

AB = CD = √17

Because AB and CD have the same length, they are congruent.

So, ABCD is a parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.