SOLVING PROBLEMS USING TRIGONOMETRIC FORMULAS

Problem 1 :

If x cos θ = y cos (θ + 2π/3) = z cos (θ + 4π/3), find the value of xy + yz + zx.

Solution :

Given that :

x cos θ = y cos (θ + 2π/3) = z cos (θ + 4π/3)

Note that xy + yz + zx = xyz(1/x + 1/y +1/z)

If we put x cos θ  =  y cos (θ+2π/3)  =  zcos(θ+4π/3) = k 

Then

1/x  =  cos θ /k  ---(1)

1/y  =  cos(θ+ 2π/3)/k ---(2)

1/z  =  cos(θ+4π/3)/k  ---(3)

(1) + (2) + (3)

(1/x) + (1/y) + (1/z)  = 

  (1/k) [ cos θ + cos(θ+ 2π/3) + cos(θ+ 4π/3) ]

=  (1/k) [ cos θ + cos θ cos 2π/3 - sin θ sin 2π/3 + cos θ cos 4π/3 - sin θ sin 4π/3]

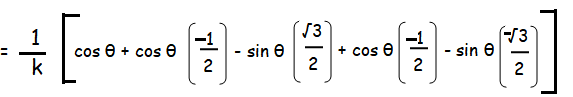
  =  0

So, the value of xy + yz + zx is 0.

Problem 2 :

Prove that :

sin(A + B) sin(A − B)  =  sin² A − sin² B

Solution :

sin (A + B)  =  sin A cos B + cos A sin B

sin (A - B)  =  sin A cos B - cos A sin B

Then, sin (A + B) sin (A - B) :

=  (sin A cos B + cos A sin B)(sin A cos B - cos A sin B)

=  sin²A cos²B - sin A sin B cos A cos B + sin A sin B cos A cos B - cos²A sin²B

=  sin²A cos²B - cos²A sin²B

=  sin²A (1-sin²B) - (1-sin²A) sin²B

=  sin²A - sin²A sin²B - sin²B + sin²A sin²B

=  sin²A - sin²B

Problem 3 :

Prove that :

cos(A + B) cos(A − B)  =  cos² A − sin² B = cos² B − sin² A

Solution :

cos(A + B)  =  cos A cos B - sin A sin B

cos(A - B)  =  cos A cos B + sin A sin B

Then, cos(A + B) cos(A - B) : 

  =  (cos A cos B - sin A sin B)(cos A cos B + sin A sin B)

  =  (cos² A cos² B + cos A sin A cos B sin B - cos A sin A cos B sin B - sin² A sin² B

=  cos² Acos² B-sin² A sin² B -----(1)

From (1), 

=  cos² A(1-sin² B)-(1 - cos² A)sin² B

=  cos² A-cos² Asin² B - sin² B + cos² Asin² B

=  cos² A - sin² B

From (1), 

=  (1-sin²A) cos² B-sin² A (1-cos² B)

=  cos² B-sin²A cos² B - sin² A + sin²A cos² B

=  cos² B - sin² A 

Hence proved.

Problem 4 :

Prove that :

sin²(A + B) - sin²(A - B)  =  sin2Asin 2B

Solution :

From (i) we have 

sin² A − sin² B  =  sin(A + B) sin(A − B) ----(1)

By comparing the given question with the formula, we get A  =  A + B and B  =  A - B

A + B  ==>  A + B + A - B  ==>  2A

A - B  ==>  A + B - (A - B) ==> 2B

Substitute 2A for (A + B) and 2B for (A - B) in (1).

(1)-----> sin²(A + B) − sin²(A − B)  =  sin2Asin 2B

Hence proved.

Problem 5 :

Prove that :

 cos 8θ cos 2θ  =  cos² 5θ − sin² 3θ

Solution :

We may write 8θ as (5θ + 3θ) and 2θ as (5θ - 3θ).

Then,

cos 8θ cos 2θ  =  cos (5θ + 3θ) cos (5θ - 3θ)

From (ii), we have

cos(A + B) cos(A − B) = cos² A − sin² B

Then, 

cos (5θ + 3θ) cos (5θ - 3θ)  =  cos² 5θ − sin² 3θ 

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.