PROVING LINES ARE PARALLEL WORKSHEET

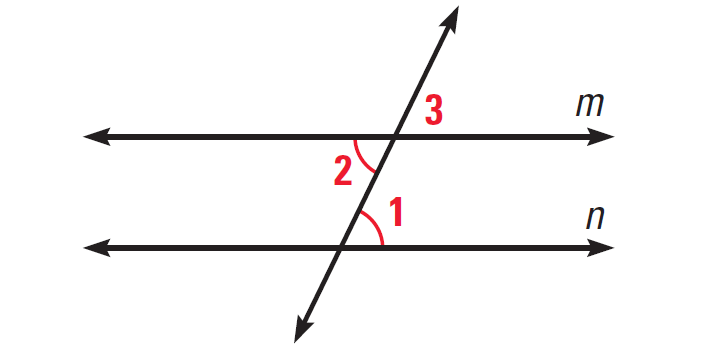
Problem 1 :

In the diagram given below, if ∠1 ≅ ∠2, then prove m||n.

Problem 2 :

In the diagram given below, if ∠4 and ∠5 are supplementary, then prove g||h.

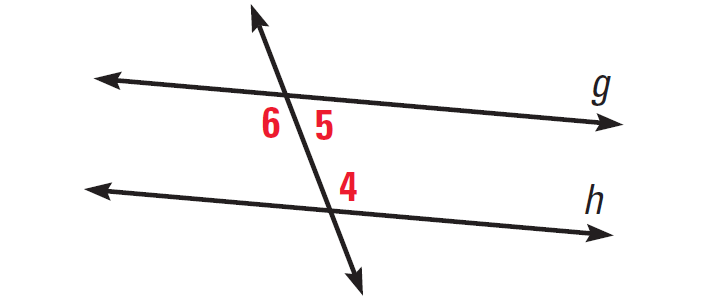
Problem 3 :

In the diagram given below, find the value of x that makes j||k.

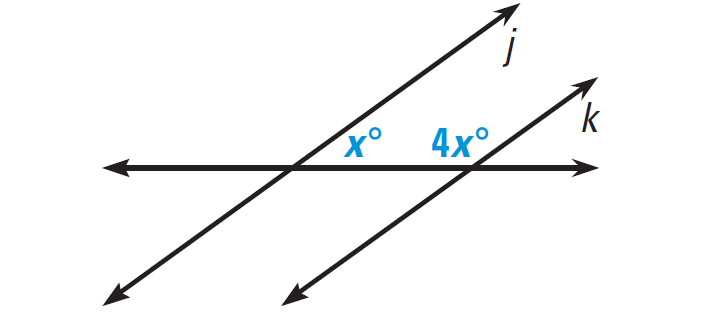
Problem 4 :

If two boats sail at a 45° angle to the wind as shown, and the wind is constant, will their paths ever cross ? Explain.

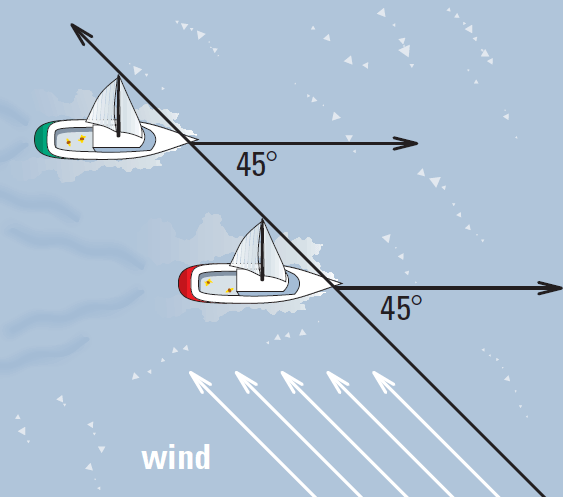
Problem 5 :

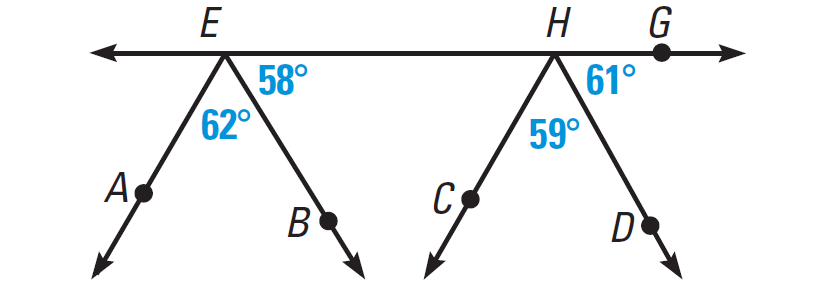
In the diagram given below, decide which rays are parallel.

(i) Is EB parallel to HD?

(ii) Is EA parallel to HC?

1. Answer :

2. Answer :

We are given that ∠4 and ∠5 are supplementary. By the linear pair postulate, ∠5 and ∠6 are also supplementary, because they form a linear pair. By the congruence supplements theorem, it follows that ∠4 ≅ ∠6. Therefore, by the alternate interior angles converse, g and h are parallel.

3. Answer :

Lines j and k will be parallel if the marked angles are supplementary.

x° + 4x° = 180°

5x = 180

x = 36

So, x = 36 makes j||k.

4. Answer :

Because corresponding angles are congruent, the paths of the boats are parallel. Parallel lines do not intersect. So the paths of the boats will never cross.

5. Answer (i) :

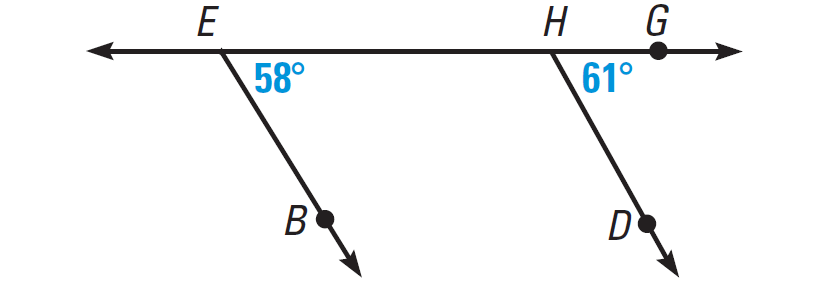
m∠BEH = 58°

m∠DHG = 61°

∠BEH and ∠DHG are corresponding angles, but they are not congruent. So EB and HD are not parallel.

5. Answer (ii) :

m∠AEH = 62° + 58° = 120°

m∠CHG = 59° + 61° = 120°

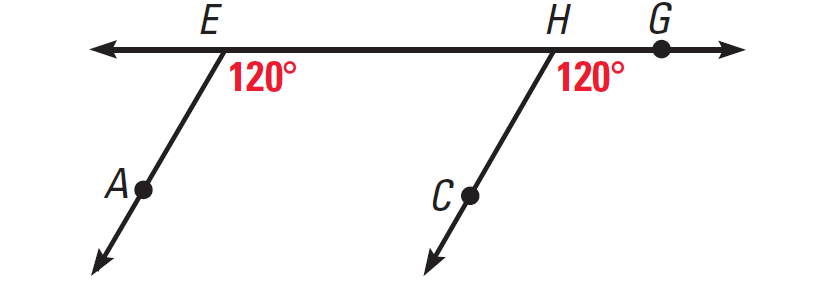
∠AEH and ∠CHG are congruent corresponding angles. So AE and CH are parallel.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.