PROPORTIONS AND SIMILAR TRIANGLES

Triangle Proportionality Theorem

If a line parallel to one side of a triangle intersects the other two sides, then it divides the two sides proportionally.

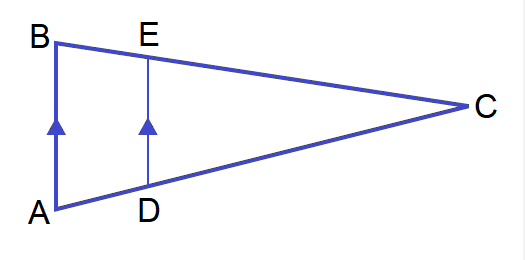
In the diagram above,

if DE ∥ AB, then CE/EB = CD/DA

Converse of the Triangle Proportionality Theorem

If a line divides two sides of a triangle proportionally, then it is parallel to the third side.

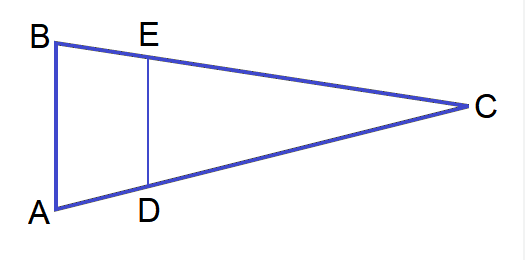
In the diagram above,

if CE/EB = CD/DA, then DE ∥ AB

Theorems on Proportionality

Theorem 1 :

If three parallel lines intersect two transversals, then they divide the transversals proportionally.

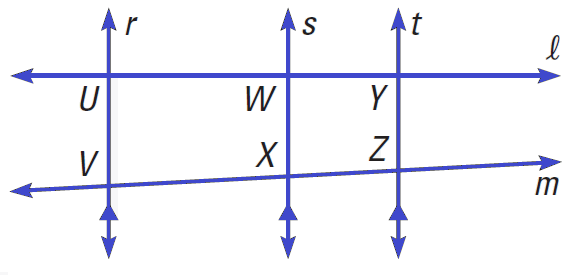
In the diagram above,

if r ∥ s and s ∥ t, and l and m intersect r, s and t, then

UW/WY = VX/XZ

Theorem 2 :

If a ray bisects an angle of a triangle, then it divides the opposite side into segments whose lengths are proportional to the lengths of the other two sides.

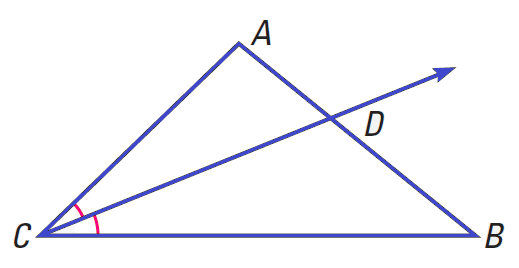
If CD bisects ∠ACB, then AD/DB = CA/CB.

Finding the Length of a Segment

Example 1 :

In the diagram shown below

PQ ∥ ST, QS = 8, SR = 4 and PT = 12

Find the length of TR.

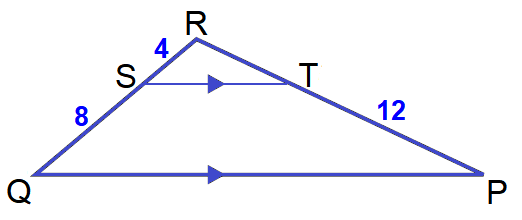
Solution :

By Triangle Proportionality Theorem,

SR/QS = TR/PT

Substitute.

4/8 = TR/12

Simplify.

1/2 = TR/12

Multiply both sides by 12.

12 ⋅ (1/2) = (TR/12) ⋅ 12

6 = TR

So,  the length of TR is 6 units.

Example 2 :

In the diagram shown below KL ∥ MN, find the values of the x and y.

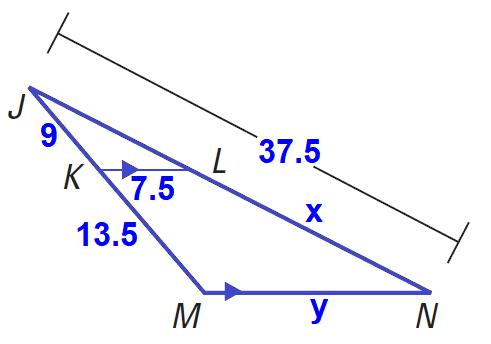
Solution :

Finding the value of x :

To find the value of x, we can set up a proportion.

Write proportion.

9/13.5 = (37.5 - x)/x

By cross product property of proportion,

9x = 13.5(37.5 - x)

9x = 506.25 - 13.5x

Add 13.5x to both sides.

22.5x = 506.25

Divide both sides by 22.5.

x = 22.5

Finding the value of y :

Since KL ∥ MN and ΔJKL ∼ ΔJMN,

JK/JM = KL/MN

JK/(JK + KM) = KL/MN

9(9 + 13.5) = 7.5/y

9/22.5 = 7.5/y

By cross product property of proportion,

9y = 7.5 ⋅ 22.5

9y = 168.75

Divide both sides by 9.

y = 18.75

Determining Parallels

Example 3 :

In the diagram shown below, determine whether MN ∥ GH.

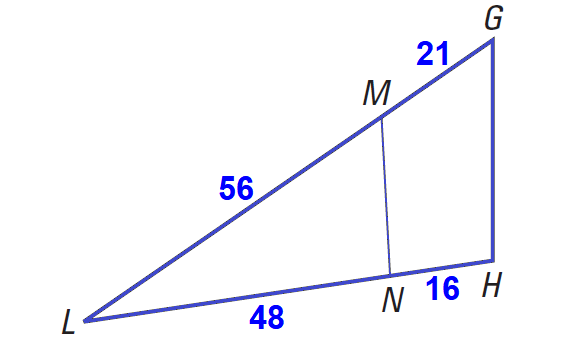
Solution :

Begin by finding and simplifying the ratios of the two sides divided by MN.

LM/MG = 56/21 = 8/3

LN/NH = 48/16 = 3/1

Because 8/3 ≠ 3/1, MN is not parallel to GH.

Using Proportionality Theorems

Example 4 :

In the diagram shown below,

∠1 ≅ ∠2 ≅ ∠3

PQ = 9, QR = 15 and ST = 11

Find the length of TU.

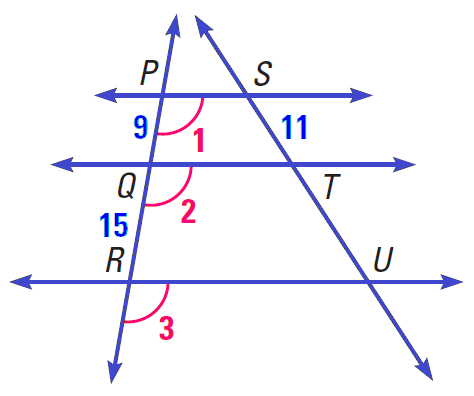
Solution :

Because corresponding angles are congruent the lines are parallel and we can use Theorem 1 on Proportionality.

Parallel lines divide transversals proportionally.

PQ/QR = ST/TU

Substitute.

9/15 = 11/TU

Simplify.

3/5 = 11/TU

By reciprocal property of proportion,

5/3 = TU/11

Multiply both sides by 11.

11 ⋅ (5/3) = (TU/11) ⋅ 11

55/3 = TU

So, the length TU is 55/3 or 18⅓ units.

Example 5 :

In the diagram shown below, ∠CAD ≅ ∠DAB. Use the given side lengths to find the length of DC.

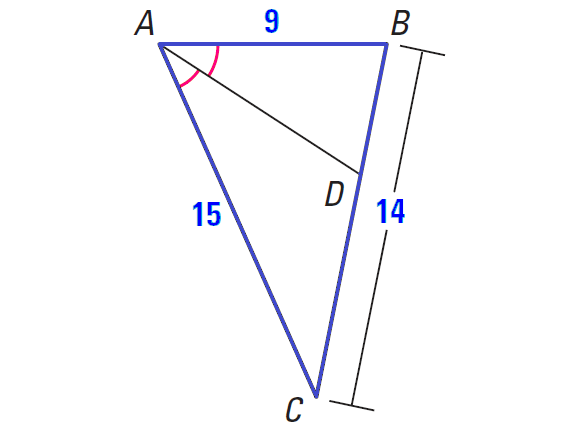
Solution :

Since AD is an angle bisector of ∠CAB, we can apply Theorem 2 on Proportionality.

Let x = DC.

Then,

BD = 14 - x

Apply Theorem 2 on Proportionality.

AB/AC = BD/DC

Substitute.

9/15 = (14 - x)/x

3/5 = (14 - x)/x

Multiply both sides by 5x.

5x ⋅ (3/5) = [(14 - x)/x] ⋅ 5x

3x = 70 - 5x

Add 5x to each side.

8x = 70

Divide both sides by 8.

x = 8.75

Hence, the length of DC is 8.75 units.

Using Proportionality Theorems in Real Life 

Example 6 :

We are insulating your attic, as shown. The vertical 2 x 4 studs are evenly spaced. Explain why the diagonal cuts at the tops of the strips of insulation should have the same lengths.

Solution :

Because the studs AD, BE and CF are each vertical, we know that they are parallel to each other. Using Theorem 8.6, you can conclude that

DE/EF = AB/BC

Because the studs are evenly spaced, we know that

DE = EF

So, we can conclude that

AB = BC

which means that the diagonal cuts at the tops of the strips have the same lengths.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.