PROPORTIONS AND SIMILAR TRIANGLES WORKSHEET

Problem 1 :

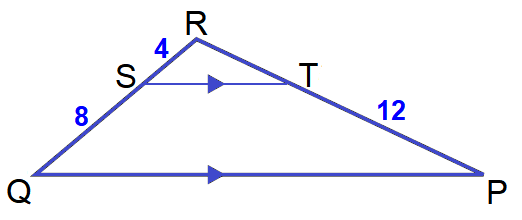
In the diagram shown below

PQ ∥ ST, QS  =  8, SR  =  4 and PT  =  12

Find the length of TR.

Problem 2 :

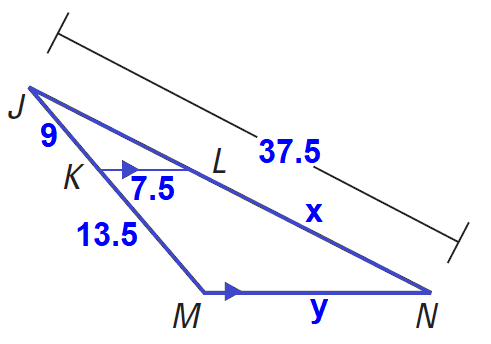
In the diagram shown below KL ∥ MN, find the values of the x and y. 

Problem 3 :

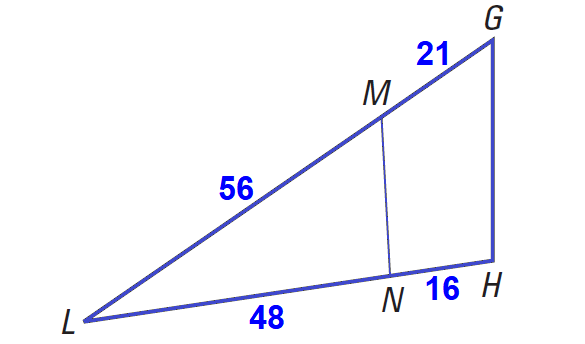
In the diagram shown below, determine whether MN ∥ GH.

Problem 4 :

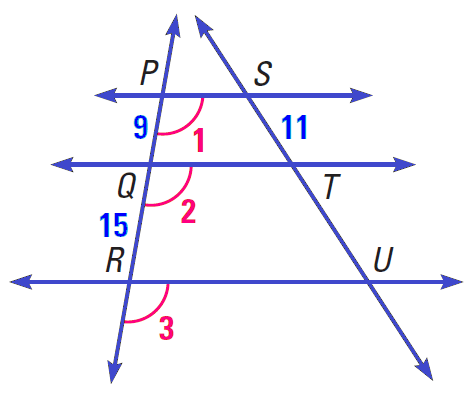
In the diagram shown below,

∠1  ≅  ∠2  ≅  ∠3

PQ  =  9, QR  =  15 and ST  =  11

Find the length of TU. 

Problem 5 :

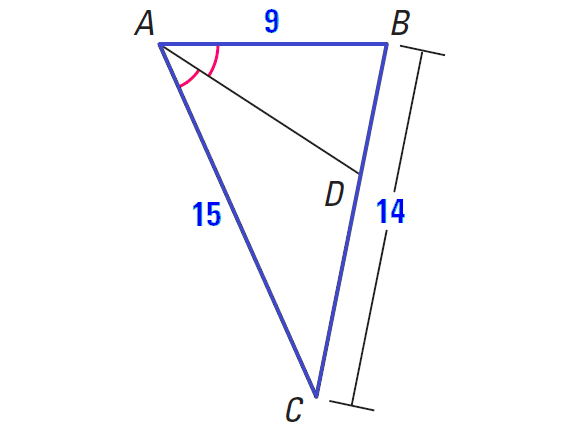
In the diagram shown below, ∠CAD  ≅  ∠DAB. Use the given side lengths to find the length of DC. 

Problem 6 :

We are insulating your attic, as shown. The vertical 2 x 4 studs are evenly spaced. Explain why the diagonal cuts at the tops of the strips of insulation should have the same lengths.

1. Answer :

By Triangle Proportionality Theorem,

SR/QS = TR/PT

Substitute.

4/8 = TR/12

Simplify.

1/2 = TR/12

Multiply both sides by 12.

12 ⋅ (1/2) = (TR/12) ⋅ 12

6 = TR

So, the length of TR is 6 units.

2. Answer :

Finding the value of x :

To find the value of x, we can set up a proportion.

Write proportion.

9/13.5 = (37.5 - x)/x

By cross product property of proportion,

9x = 13.5(37.5 - x)

9x = 506.25 - 13.5x

Add 13.5x to both sides.

22.5x = 506.25

Divide both sides by 22.5.

x = 22.5

Finding the value of y :

Since KL ∥ MN and ΔJKL ∼ ΔJMN,

JK/JM = KL/MN

JK/(JK + KM) = KL/MN

9(9 + 13.5) = 7.5/y

9/22.5 = 7.5/y

By cross product property of proportion,

9y = 7.5 ⋅ 22.5

9y = 168.75

Divide both sides by 9.

y = 18.75

3. Answer :

Begin by finding and simplifying the ratios of the two sides divided by MN.

LM/MG = 56/21 = 8/3

LN/NH = 48/16 = 3/1

Because 8/3 ≠ 3/1, MN is not parallel to GH.

4. Answer :

Because corresponding angles are congruent the lines are parallel and we can use Theorem 1 on Proportionality.

Parallel lines divide transversals proportionally.

PQ/QR = ST/TU

Substitute.

9/15 = 11/TU

Simplify.

3/5 = 11/TU

By reciprocal property of proportion,

5/3 = TU/11

Multiply each side by 11.

11 ⋅ (5/3) = (TU/11) ⋅ 11

55/3 = TU

Hence, the length TU is 55/3 or 18⅓ units.

5. Answer :

Since AD is an angle bisector of ∠CAB, we can apply Theorem 2 on Proportionality.

Let x = DC. Then,

BD = 14 - x

Apply Theorem 2 on Proportionality.

AB/AC = BD/DC

Substitute.

9/15 = (14 - x)/x

3/5 = (14 - x)/x

Multiply both sides by 5x.

5x ⋅ (3/5) = [(14 - x)/x] ⋅ 5x

3x = 70 - 5x

Add 5x to each side.

8x = 70

Divide both sides by 8.

x = 8.75

Hence, the length of DC is 8.75 units.

6. Answer :

Because the studs AD, BE and CF are each vertical, we know that they are parallel to each other. Using Theorem 8.6, you can conclude that

DE/EF = AB/BC

Because the studs are evenly spaced, we know that

DE = EF

So, we can conclude that

AB = BC

which means that the diagonal cuts at the tops of the strips have the same lengths.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.