PROPERTIES OF DEFINITE INTEGRALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
By the second fundamental theorem of integral calculus, the following properties of definite integrals hold. They are stated here without proof.
Property 1 :
Definite integral is independent of the change of variable.
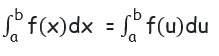
Property 2 :
The value of the definite
integral changes by minus sign if the limits are interchanged
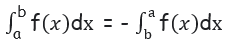
Property 3 :
Property 4 :
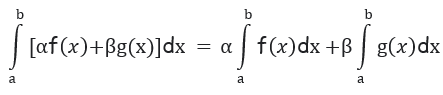
Property 5 :
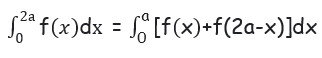
Property 6 :
If f(x) is even function, then
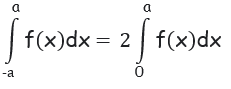
Property 7 :
If f(x) is odd function, then
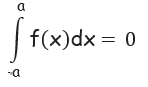
Property 8 :
If f(2a-x) = f(x)
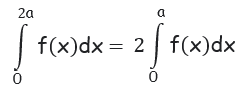
Property 9 :
If f(2a-x) = -f(x)
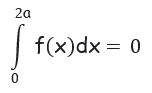
Property 10 :
If f(a-x) = f(x)
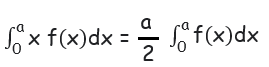
This property help us to remove the factor x present in the integrand of the LHS.
Example Problems Using Properties of Definite Integral
Problem 1 :
Evaluate the following integrals using properties of integration :
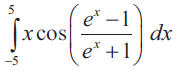
Solution :
Let f(x) = x cos [(ex-1)/(ex+1)]
Apply x = -x
f(-x) = -x cos [(e-x-1)/(e-x+1)]
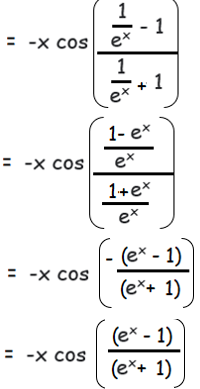
f(-x) = -f(x)
The given function f(x) is odd function. So, the value is 0.
Problem 2 :
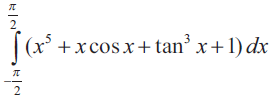
Solution :
Let f(x) = x5 + x cos x + tan3x + 1
Apply x = -x
f(-x) = -x5 -x cos x - tan3x + 1
|
f(x) = x5 f(-x) = (-x)5 f(-x) = -x5 |
f(x) = x cos x f(-x) = -x cos (-x) f(-x) = -x cos x |
f(x) = tan3x
f(-x) = [tan(-x)]3
f(-x) = -tan3x
So, x5, x cos x and tan3x are odd functions. By integrating them we will get 0.
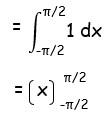
= π/2+π/2
= 2π/2
= π
Problem 3 :
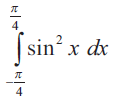
Solution :
Let f(x) = (sin x)2
Apply x = -x
f(-x) = (sin (-x))2
f(-x) = (-sin x)2
f(-x) = sin2x
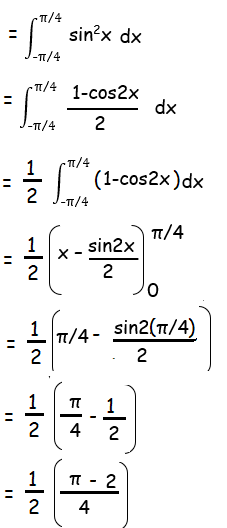
Problem 4 :
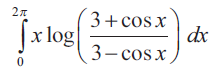
Solution :
Let f(x) = x log [(3+cosx)/(3-cosx)]
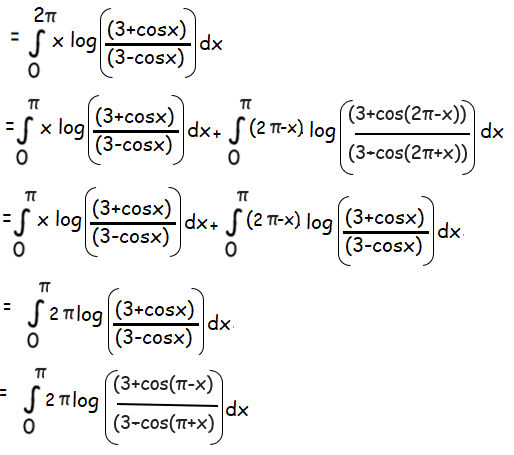
Let g(π-x) = 2π [log (3+cos(π-x))- log (3-cos(π-x))]
= 2π [log (3-cosx) - log (3+cosx)]
= -2π [log (3+cosx) - log (3+cosx)]
g(-x) = -g(x)
So, the value is 0.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems