PROPERTIES OF TRIANGLE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Can the following measures be the lengths of sides of a triangle?
6 in. 3 in and 7 in.
Problem 2 :
Can the following measures be the lengths of sides of a triangle?
6 cm, 10 cm and 3 cm
Problem 3 :
Can the following angle measures be the interior angles of a triangle?
35°, 45° and 100°
Problem 4 :
Can the following angle measures be the interior angles of a triangle?
42°, 73° and 88°
Problem 5 :
Which is the longest side of a right triangle?
Problem 6 :
Can you have a triangle with all the three angles equal to 60º? Explain.
Problem 7 :
Can you have a triangle with all the three angles less than 60º? Explain.
Problem 8 :
Can you have a triangle with all the three angles greater than 60º? Explain.
Problem 9 :
Can you have a triangle with two right angles? Explain.
Problem 10 :
Can you have a triangle with two obtuse angles? Explain.
Problem 11 :
Can you have a triangle with two acute angles? Explain.
Problem 12 :
If the lengths of two sides of a triangle are 14 and 9, find one possible value which can be the length of the third side. Justify your answer.
Problem 13 :
Find the length of the hypotenuse of a right triangle, if the lengths of the other two sides are 3 cm. and 4 cm.
Problem 14 :
The length of the hypotenuse of a triangle is 10 cm and sum of the lengths of the remanning two sides is 14 cm. Find the lenght of each of the remaning two sides.

Answers
1. Answer :
Property : Sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
If the given measures are the lengths of sides of a triangle, sum of any two measures must be greater than the third measure.
6 in. + 3 in. > 7 in.
3 in. + 7 in. > 6 in.
6 in. + 7 in. > 3 in.
Since the given measures satisfy the above property of triangle, they can be the lengths of sides of a triangle.
2. Answer :
6 cm + 10 cm > 3 cm
10 cm + 3 cm > 6 cm
6 cm + 3 cm < 10 cm
Sum of the first measure (6 cm) and the third measure (3 cm) is not greater then the second measure (10 cm).
The given three measures do not satisfy the property mentioned in 1. Answer above. So, they can not be the lengths of sides of a triangle.
3. Answer :
Property : Sum of the interior angles of a triangle is equal to 180°.
35° + 45° + 100° = 180°
Since the given angle measures satisfy the above property, they can be the interior angles of a triangle.
4. Answer :
42° + 73° + 88° = 203° ≠ 180°
Since the given angle measures do not satisfy the property mentioned in 3. Answer above, they CAN NOT be the interior angles of a triangle.
5. Answer :
Hypotenuse (opposite to right angle) is the longest side of a right angle.
6. Answer :
Yes, we can
60º + 60º + 60º = 180º
The property mentioned in 3. Answer above is satisfied. So, we can have a triangle with all the three angles equal to 60º
7. Answer :
No. we can't
In 5. Answer above, we have seen that if all the three angles equal to 60º, then the sum of the three angles equal to 180º.
Even if one of the angles is less than 60º, then the sum of the three angles will be less than 180º and the property mentioned in 3. Answer will not be satisfied.
So, we can not have a triangle with all the three angles less than 60º.
8. Answer :
No. we can't
In 5. Answer above, we have seen that if all the three angles equal to 60º, then the sum of the three angles equal to 180º.
Even if one of the angles is greater than 60º, then the sum of the three angles will be greater than 180º and the property mentioned in 3. Answer will not be satisfied.
So, we can not have a triangle with all the three angles greater than 60º.
9. Answer :
No. we can't
Let us assume a triangle with two right angles and third angle x.
90º + 90º + x = 180º
180º + x = 180º
Subtract 180º from both sides.
x = 0º
In a triangle, if two angles are right angles, then the third angle is 0º.
It's impossible to have one of the angles of a triangle as 0º. Because each angle of a triangle is greater than zero,
So, we can not have a triangle with two right angles.
10. Answer :
No. we can't
Obtuse angle is an angle which is greater than 90º.
In a triangle, if there are two obstuse angles, then then sum of those two angles equal to greater than 180º. If third angle is included, the sum of the three angles will still be greater than 180º.
Example :.
91º + 92º + 93º = 276º
The property mentioned in 3. Answer is not satisfied.
So, we can not have a triangle with two obstuse angles.
11. Answer :
Yes, we can
Acute angle is an angle which is less than 90º.
In a triangle, if there are two acute angles, then then sum of those two angles equal to less than 180º. A third can be included such that the sum of the three angles equal to 180º.
Example :
20º + 30º + 130º = 180º
The property mentioned in 3. Answer is satisfied.
So, we can have a triangle with two acute angles.
12. Answer :
Let x be the length of third side of the triangle.
Lengths of the given two sides are 14 and 9.
Difference of the lengths = 14 - 9 = 5
Sum of the lengths = 14 + 9 = 23
The range of possible measures for the length of the third side :
5 < x < 23
The length of the third side is any value between 5 and 23.
One possible value for the length of third side is 6.
Justification :
Three sides of the triangle are
14, 9 and 6
14 + 9 > 6
9 + 6 > 14
14 + 6 > 9
The property mentioned in 1. Answer above is satisfied. Hence, the answer is justified.
13. Answer :
From the given information we can draw the triangle as shown below.
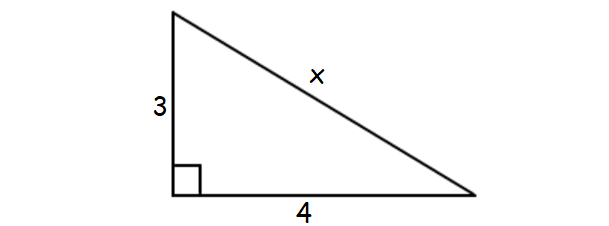
In the above triangle, we have to find the value of x.
According to Pythagorean theorem, square of the hypotenuse is equal to the sum of the squares of other two sides.
x2 = 42 + 32
x2 = 16 + 9
x2 = 25
x = 5
The length of the hypotenuse is 5 cm.
14. Answer :
Let x be the length of one of the two remaning sides.
Then, the length of the other side is (14 - x).
Using The Pythagorean Theorem,
x2 + (14 - x)2 = 102
x2 + (14 - x)(14 - x) = 100
x2 + 196 - 14x - 14x + x2 = 100
2x2 - 28x + 196 = 100
2x2 - 28x + 96 = 0
Divide both sides by 2.
x2 - 14x + 48 = 0
Solve by factoring.
x2 - 8x - 6x + 48 = 0
x(x - 8) - 6(x - 8) = 0
(x - 8)(x - 6) = 0
x - 8 = 0 or x - 6 = 0
x = 8 or x = 6
If x = 8,
= 14 - x
= 14 - 8
= 6
If x = 6,
= 14 - x
= 14 - 6
= 8
The lengths of the remaining two sides are 6 cm and 8 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
