PROPERTIES OF TRANSLATIONS

When we translate something in geometry, we are simply moving it around. We don't distort it anyway. If we translate a segment, it remains a segment and its length doe not change.

Similarly, if we translate an angle, the measure of the angle does not change. 

Properties of Translations

The following are the three basic properties of translations :

1.  Line segments are taken to line segments of same length.

2.  Angles are  taken to angles of the same measure. 

3.  Lines are taken to lines, and parallel lines are taken to parallel lines. 

From the above three basic properties, we can derive the following results. 

(i)  The original figure and its image are congruent and also identical in every aspect for their position. 

(ii)  Line segments linking a vertex in the original figure to the corresponding vertex in the image are congruent and parallel.

Example : 

Trapezoid ABCD has the vertices A (1, 0), B(4, 0), C(4, -4) and D(0, -4). Translate your trapezoid 5 units to the left and 3 units up. Determine whether the trapezoid ABCD and its translated image satisfy the properties of translations. 

Solution : 

Step 1 :

Let A', B', C' and D' be the vertices of the translated figure.

Since there is a translation of 5 units to the left and 3 units up , we have to subtract 5 from x-coordinate and add 3 to y-coordinate of each vertex. 

A' ------>  (1-5, 0+3)  =  (-4, 3)

B' ------>  (4-5, 0+3)  =  (-1, 3)

C' ------>  (4-5, -4+3)  =  (-1, -1)

D' ------>  (0-5, -4+3)  =  (-5, -1)

Step 2 :

Sketch trapezoid ABCD and its image A'B'C'D'.

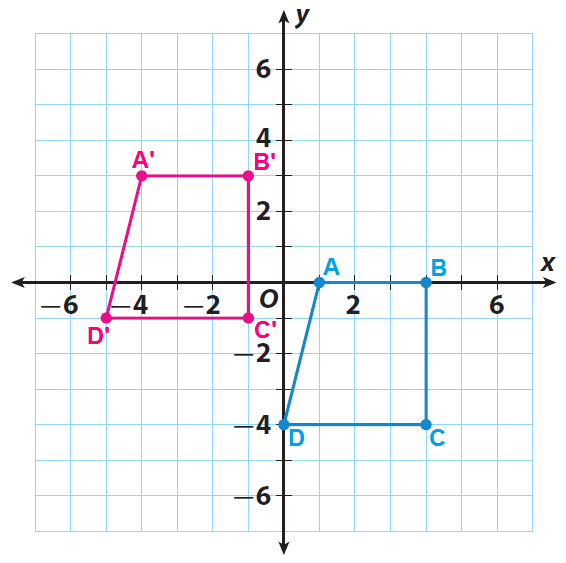
Step 3 : 

Use a ruler to measure the corresponding sides of trapezoid  ABCD and its image A'B'C'D' in centimeters.

AB  =  A'B'  =  1.3 cm

BC  =  B'C'  =  1.7 cm

CD  =  C'D'  =  1.7 cm

AC  =  A'C'  =  1.75 cm

The lengths of corresponding sides are the same.

So, trapezoid ABCD and its image A'B'C'D' satisfy the first basic property of translations, that is, "Line segments are taken to line segments of same length".

Step 4 : 

Use a protractor to measure the corresponding angles of trapezoid  ABCD and its image A'B'C'D' in centimeters.

m∠A  =  m∠A'  =  104°

m∠B  =  m∠B'  =  90°

m∠C  =  m∠C'  =  90°

m∠D  =  m∠D'  =  76°

The measures of corresponding angles are the same.

So, trapezoid ABCD and its image A'B'C'D' satisfy the second basic property of translations, that is, "Angles are  taken to angles of the same measure".

Step 5 : 

In trapezoid ABCD, the lines AB and CD are parallel. Because they both lie along horizontal grid lines. Similarly, in the image A'B'C'D', the lines A'B' and C'D' are parallel.

The sides which are parallel in the trapezoid ABCD  remain parallel in its image A'B'C'D'. 

And also, the lines BC and AD are taken to the lines B'C' and A'D' respectively.  

So, trapezoid ABCD and its image A'B'C'D' satisfy the third basic property of translations, that is, "Lines are taken to lines, and parallel lines are taken to parallel lines".

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.