PROPERTIES OF SQUARE ROOTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. If two or more numbers multiplied with square roots, you can take the square root once and multiply the numbers inside the square root.
√m x √n = √(m x n)
2. If two numbers are in division with square roots, you can take the square root once and divide the numbers inside the square root.
√m/√n = √(m/n)
3. One number can be taken out of the square root for every two same numbers multiplied inside the square root.
√(m x m) = m
√4 = √(2 x 2) = 2
4. Square root of a number can be written as exponent 1/2.
√m = m1/2
5. Addition and subtraction of two or more numbers with square roots can be performed with like radicands only. (Radicand is the number inside the square root)
For example, 9√2 and 4√2 can be added or subtracted. Because the numbers inside the square roots are same.
9√2 + 4√2 = 13√2
9√2 - 4√2 = 5√2
6. If a square root is moved from side of the equation to the other side, it will become square.
√x = a
x = a2
7. If a square is moved from side of the equation to the other side, it will become square root.
y2 = b
y = √b
8. If the digit in one's place of a number is 2, 3, 7 or 8, then the number can not be a perfect square. So the square root of such numbers will be irrational.
For example, √23 = 4.795831.........
9. If a number ends with odd number of zeros, then, the square root of the number will be irrational.
For example, √3000 = 54.772255.......
10. The square of a perfect square is always a rational number.
√4 = √(2 x 2) = 2
√49 = (7 x 7) = 7
11. The square root of an even perfect square number is always even and the square root of an odd perfect square number is always is odd.
For example,
√144 = 144
√225 = 15
12. Square root of a negative number is considered to be an imaginary value.
For example, √(-9), √(-12).
Solved Problems
Problem 1 :
Simplify :
√6 ⋅ √3
Solution :
= √6 ⋅ √3
= √(6 ⋅ 3)
= √(2 ⋅ 3 ⋅ 3)
= 3√2
Problem 2 :
Simplify :
√35 ÷ √7
Solution :
= √35 ÷ √7
= √(35/7)
= √5
Problem 3 :
Simplify :
3√425 + 4√68
Solution :
Decompose 425 and 68 into prime factors using synthetic division.
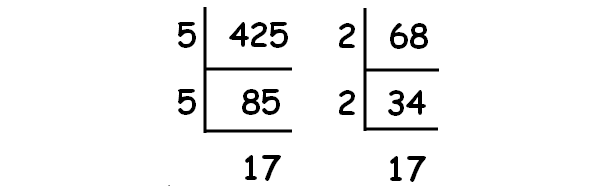
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
3√425 + 4√68 :
= 3(5√17) + 4(2√17)
= 15√17 + 8√17
= 23√17
Problem 4 :
Simplify :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
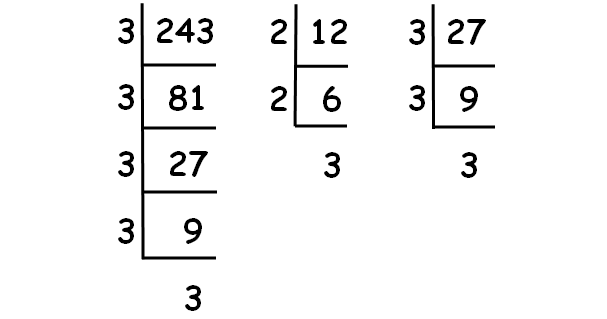
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
Problem 5 :
If √a = 1/5, then find the value of a.
Solution :
√a = 1/5
a = (1/5)2
a = 12/52
a = 1/25
Problem 6 :
If (√4)7 ⋅ (√2)-4 = 2k, then solve for k.
Solution :
(√4)7 ⋅ (√2)-4 = 2k
27 ⋅ (21/2)-4 = 2k
27 ⋅ 2-2 = 2k
27 - 2 = 2k
25 = 2k
k = 5
Problem 7 :
. Using properties of squares and square roots calculate:
1002 − 982
Solution :
= √(1002 − 982)
= √(100 + 98) (100 - 98)
= √198 (2)
= √(2 x 3 x 3 x 11 x 2)
= 2 x 3 √11
= 6√11
Problem 8 :
By what least number should 2028 be multiplied so that the product is a perfect square? Find the square root of the product so obtained.
Solution :
2028 is not a perfect square, by multiplying some numerical value by this we can change it as perfect square.
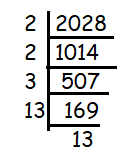
= √(2 x 2 x 3 x 13 x 13)
By grouping as pairs, we have 3 which doesn't have pair. Then 3 is the number to be multiplied to make it as perfect square.
Problem 9 :
By what least number should 3528 be divided so that the quotient is a perfect square? Find the square root of the quotient so obtained
Solution :

3528 is not a perfect square, by removing some numerical value from 3528 we can make as perfect square.
To find the number which should be removed, we have to decompose into product of prime factors.
= √(2 x 2 x 2 x 3 x 3 x 7 x 7)
Since 2 is the number which doesn't have pair, we have to remove 2. So, 2 is the number to be removed.
= √(2 x 2 x 3 x 3 x 7 x 7)
= 2 x 3 x 7
= 42
The square root of the quotient is 42.
Problem 10 :
Express 16 as sum of odd numbers.
Solution :
1 = 1
4 = 1 + 3
9 = 1 + 3 + 5
16 = 1 + 3 + 5 + 7
Problem 11 :
Find the least perfect square number which is divisible by each of the numbers 8, 12, 15 and 20.
Solution :
LCM of (8, 12, 15, 20)
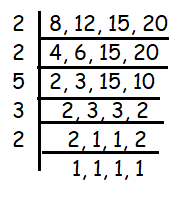
LCM (8, 12, 15, 20) = 2 x 2 x 5 x 3 x 2
= 120
120 is divisible by 8, 12 and 20, but not divisible by 15.
120 x 2 ==> 240
To make this as perfect square,
2 x 2 x 2 x 2 x 5 x 5 x 3 x 3
= 3600
So, the required number is 3600.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

