PROPERTIES OF SQUARE ROOTS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1-6 : Simplify.
Question 1 :
√2 ⋅ √6
Question 2 :
5√6 ⋅ 3√8
Question 3 :
√32 ÷ √8
Question 4 :
5√8 ÷ 2√2
Question 5 :
3√425 + 4√68
Question 6 :
√243 - 5√12 + √27
Question 7 :
If √x = ½, then find the value of x.
Question 8 :
If (√9)5 ⋅ (√3)-6 = 3y, then solve for y.
Question 9 :
Solve for x :
x2 = 25
Question 10 :
Solve for y :
3y2 - 4 = 104

Answers
1. Answer :
= √2 ⋅ √6
= √(2 ⋅ 6)
= √(2 ⋅ 2 ⋅ 3)
= 2√3
2. Answer :
= 5√6 ⋅ 3√8
= (5 ⋅ 3)(√6 ⋅ √8)
= 15√(6 ⋅ 8)
= 15√(2 ⋅ 3 ⋅ 2 ⋅ 2 ⋅ 2)
= 15[2 ⋅ 2 ⋅ √3]
= 15(4√3)
= 60√3
3. Answer :
= √32 ÷ √8
= √(³²⁄₈)
= √4
= √(2 ⋅ 2)
= 2
4. Answer :
= 5√8 ÷ 2√2
= (⁵⁄₂)√(⁸⁄₂)
= (⁵⁄₂)(√4)
= (⁵⁄₂)(2)
= 5
5. Answer :
Decompose 425 and 68 into prime factors using synthetic division.
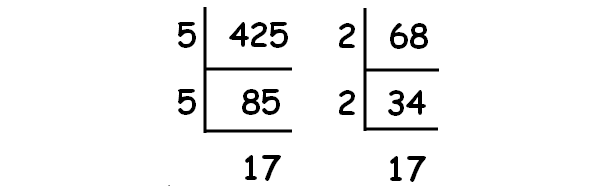
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
3√425 + 4√68 :
= 3(5√17) + 4(2√17)
= 15√17 + 8√17
= 23√17
6. Answer :
Decompose 243, 12 and 27 into prime factors using synthetic division.
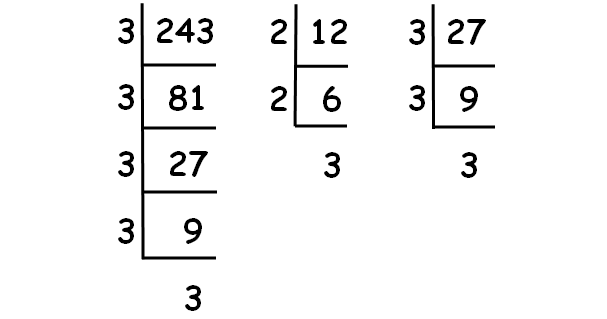
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
7. Answer :
√x = ½
Take square on both sides.
(√x)2 = (½)2
x = 12/22
x = ¼
8. Answer :
(√9)5 ⋅ (√3)-6 = 3y
35 ⋅ (3½)-6 = 3y
35 ⋅ 3-3 = 3y
35 - 3 = 3y
32 = 3y
y = 2
9. Answer :
x2 = 25
Take square root on both sides.
√x2 = ±√25
x = ±√(5 ⋅ 5)
x = ±5
x = -5 or x = 5
10. Answer :
3y2 - 4 = 104
Add 4 to both sides.
3y2 = 108
Divide both sides by 3.
y2 = 36
Take square root on both sides.
√y2 = ±√36
y = ±√(6 ⋅ 6)
y = ±6
y = -6 or y = 6
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems -
Coin Tossing Probability
Dec 23, 25 11:29 PM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems -
Permutation and Combination
Dec 23, 25 11:28 PM
Permutation and Combination - Definition - Formulas - Shortcuts - Difference between permutation and combination
