PROPERTIES OF SET OPERATIONS

Problem 1 :

For the given sets

A = {-10, 0, 1, 9, 2, 4, 5}

B = {-1, -2, 5, 6, 2, 3, 4},

Verify the following :

(i) Set union is commutative. Also verify it by using Venn diagram. 

(ii) Set intersection is commutative. Also verify it by using Venn diagram.

Solution :

(i) Let us verify that union is commutative. 

A u B  =  {-10, 0, 1, 9, 2, 4, 5} u {-1, -2, 5, 6, 2, 3, 4}

A u B  =  {-10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ---------(1)

B u A  =  {-1, -2, 5, 6, 2, 3, 4 } u {-10, 0, 1, 9, 2, 4, 5} 

B u A  =  {-10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ---------(2)

From (1) and (2), we have 

A u B  =  B u A

By Venn diagram, we have 

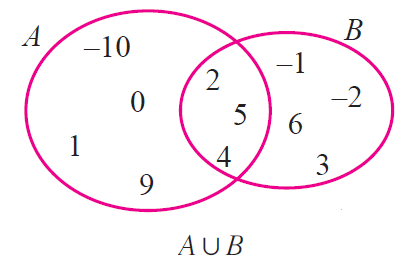
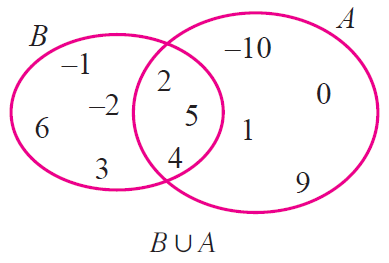
From the above two Venn diagrams, it is clear that 

A u B  =  B u A

Hence, it is verified that set union is commutative.

(ii) Let us verify that union is commutative. 

A n B  =  {-10, 0, 1, 9, 2, 4, 5} n {-1, -2, 5, 6, 2, 3, 4}

A n B  =  {2, 4, 5} ---------(1)

B n A  =  {-1, -2, 5, 6, 2, 3, 4 } u {-10, 0, 1, 9, 2, 4, 5} 

B n A  =  {2, 4, 5} ---------(2)

From (1) and (2), we have 

A n B  =  B n A

By Venn diagram, we have 

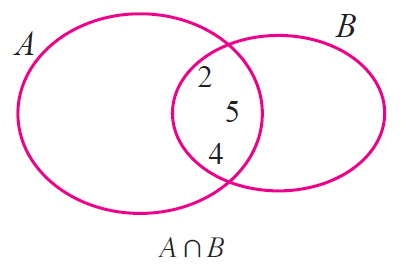
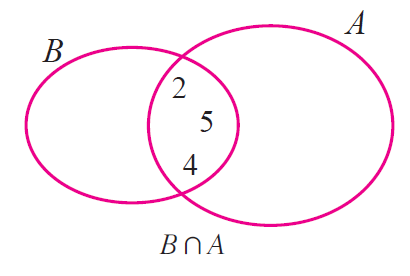
From the above two Venn diagrams, it is clear that 

A n B  =  B n A

Hence, it is verified that set intersection is commutative.

Problem 2 :

For the given sets

A  =  {1, 2, 3, 4, 5}

B  =  {3, 4, 5, 6}

C  =  {5, 6, 7, 8}

verify that

A u (B u C )  =  (A u B) u C

Also verify it by using Venn diagram. 

Solution :

Let us verify that set union is associative. 

B u C  =  {3, 4, 5, 6} u {5, 6, 7, 8}

B u C  =  {3, 4, 5, 6, 7, 8}

A u (B u C)  =  {1, 2, 3, 4, 5} u {3, 4, 5, 6, 7, 8} 

A u (B u C)  =  {1, 2, 3, 4, 5, 6, 7, 8} ---------(1)

A u B  =  {1, 2, 3, 4, 5} u {3, 4, 5, 6}

A u B  =  {1, 2, 3, 4, 5, 6}

(A u B) u C  =  {1, 2, 3, 4, 5, 6} u {5, 6, 7, 8} 

(A u B) u C  =  {1, 2, 3, 4, 5, 6, 7, 8} ---------(2)

From (1) and (2), we have 

A u (B u C)  =  (A u B) u C

By Venn diagram, we have 

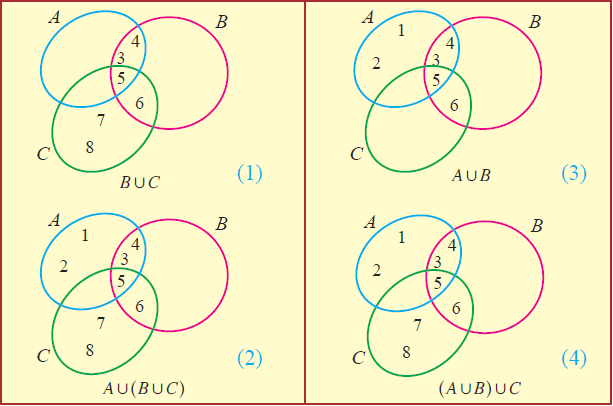
From the above Venn diagrams (2) and (4), it is clear that 

A u (B u C)  =  (A u B) u C

Hence, it is verified that set union is associative.

Problem 3 :

For the given sets

A  =  {a, b, c, d}

B  =  {a, c, e}

C  =  {a, e}

verify that

A n (B n C)  =  (A n B) n C

Also verify it by using Venn diagram. 

Solution :

Let us verify that set intersection is associative. 

B n C  =  {a, c, e} u {a, e}

B n C  =  {a, e}

A n (B n C)  =  {a, b, c, d} n {a, e} 

A n (B n C)  =  {a} ---------(1)

A n B  =  {a, b, c, d} u {a, c, e}

A n B  =  {a, c}

(A n B) n C  =  {a, c} n {a, e} 

(A n B) n C  =  {a} ---------(2)

From (1) and (2), we have 

A n (B n C)  =  (A n B) n C

By Venn diagram, we have 

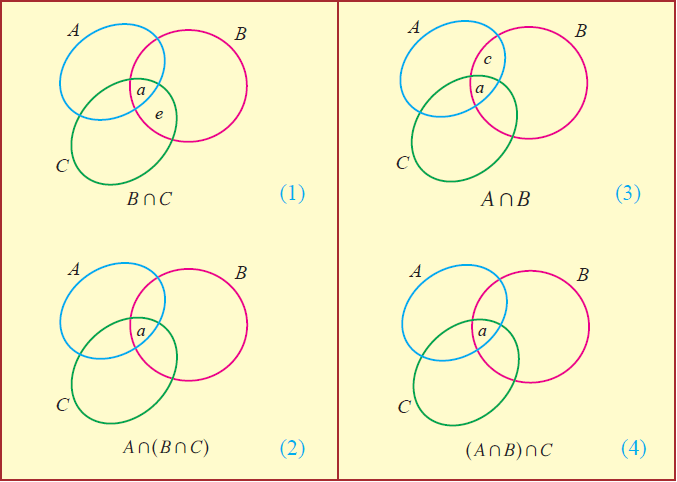
From the above Venn diagrams (2) and (4), it is clear that 

A n (B n C)  =  (A n B) n C

Hence, it is verified that set intersection is associative.

Problem 4 :

For the given sets

A  =  {0, 1, 2, 3, 4}

B  =  {1, -2, 3, 4, 5, 6}

C  =  {2, 4, 6, 7}

verify that

A u (B n C )  =  (A u B) n (A u C)

Also verify it by using Venn diagram. 

Solution :

Let us verify that union distributes over intersection. 

B n C  =  {1, -2, 3, 4, 5, 6} n {2, 4, 6, 7}

B n C  =  {4, 6}

A u (B n C)  =  {0, 1, 2, 3, 4} u {4, 6} 

A u (B n C)  =  {0, 1, 2, 3, 4, 6} -----(1)

A u B  =  {0, 1, 2, 3, 4} u {1, -2, 3, 4, 5, 6}

A u B  =  {-2, 0, 1, 2, 3, 4, 5, 6}

A u C  =  {0, 1, 2, 3, 4 } u {2, 4, 6, 7}

A u C  =  {0, 1, 2, 3, 4, 6, 7}

(A u B)n(A u C) = {-2, 0, 1, 2, 3, 4, 5, 6}n{0, 1, 2, 3, 4, 6, 7}

(A u B) n (A u C)  =  {0, 1, 2, 3, 4, 6} ---------(1)

From (1) and (2), we have 

A u (B n C)  =  (A u B) n (A u C)

By Venn diagram, we have 

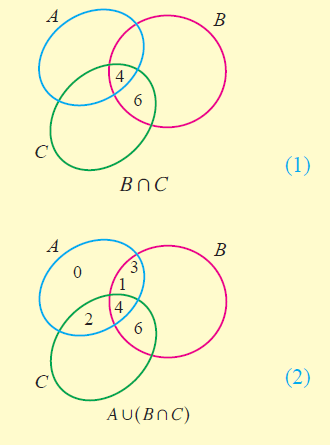
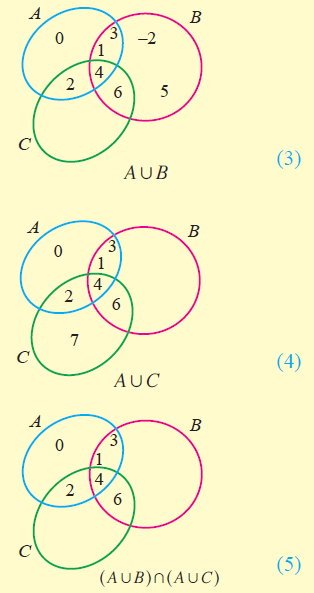
From the above Venn diagrams (2) and (5), it is clear that 

A u (B n C)  =  (A u B) n (A u C)

Hence, it is verified that union distributes over intersection.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.