PROPERTIES OF SCALAR PRODUCT OR DOT PRODUCT

Property 1 :

Scalar product of two vectors is commutative.

With usual definition,

a vector ⋅ b vector  = |a||b|cos θ  = |b||a|cos θ = b ⋅ a

That is, for any two vectors a and b, a ⋅ b = b ⋅ a

Property 2 :

Nature of scalar product.

We know that 0 ≤  θ ≤ π

If θ = 0 then a ⋅ b = ab

[Two vectors are parallel in the same direction then θ = 0]

If θ = π then a ⋅ b = −ab

[Two vectors are parallel in the opposite direction θ = π/2

• If θ = π/2 then a vector ⋅ b vector[Two vectors are perpendicular θ = π/2].
• If 0 < θ < π/2 then cosθ is positive and hence a ⋅ b is positive. 
• If π/2 < θ < π then cos  is negative and hence a ⋅ b is negative.

That is a vector ⋅ b vector is 

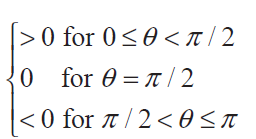
Property 3 :

When is a scalar/dot product of two vectors equal to zero ?

a vector ⋅ b vector  =  0

when |a vector|  =  0 |(or) |b vector|  =  0 or θ = π/2

Property 4 :

If the dot product of two nonzero vectors is zero, then the vectors are perpendicular. 

For any two non-zero vectors a vector and b vector, a ⋅ b = 0 a vector is perpendicular to b vector.

Property 5 :

Different ways of representations of a vector ⋅ b vector

a vector ⋅ a vector =|a vector|² = (a vector)² = (a vector)² = a²

These representations are essential while solving problems

Property 6 :

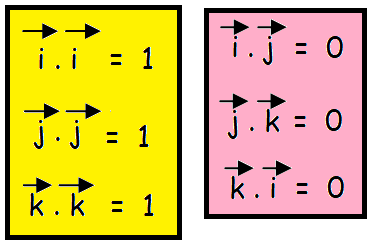
For any two scalars λ and μ

λa vector ⋅ μb vector =  λμ (a vector ⋅ b vector) = (λμa vector) ⋅ b vector = a vector ⋅ (λμb vector)

Property 7 :

Scalar product is distributive over vector addition.

That is, for any three vectors a, b, c.

a vector (b vector + c vector) = a ⋅ b + a ⋅ c (Left distributivity)

(a vector + b vector) ⋅ c vector  =  a ⋅ c + b ⋅ c (Right distributivity)

Subsequently,

a vector ⋅ (b vector − c vector) = a vector ⋅ b vector  - a vector ⋅ c vector

and (a vector − b vector) ⋅ c vector  =  a vector ⋅ c vector − b vector ⋅ c vector

These can be extended to any number of vectors

Property 8 :

Vector identities :

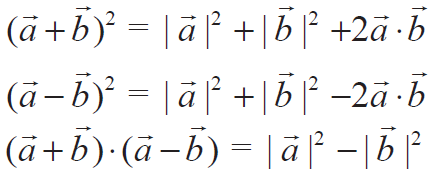
Property 9 :

Working rule to find scalar product of two vectors.

Let

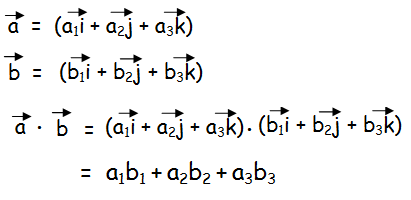
Hence, the scalar product of two vectors is equal to the sum of the products of their corresponding rectangular components.

Property 10 :

Angle between two vectors

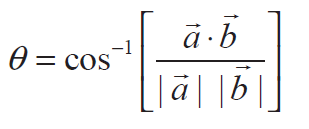
Property 11 :

For any two vectors and a vector b vector

|a vector + b vector|  ≤ |a vector| + |b vector|

We know that if a vector and b vector are the two sides of a triangle then the sum a vector + b vector represents the third side of the triangle. Therefore, by triangular property, |a vector + b vector|  ≤ |a vector| + |b vector|

Property 12 :

For any two vectors and, |a vector ⋅ b vector|  ≤  |a vector| |b vector|.

If one of them is zero vector then the equality holds. So, let us assume that both are non-zero vectors.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.