PROPERTIES OF ROTATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A rotation is a transformation that turns a figure around a given point called the center of rotation. The image has the same size and shape as the pre-image. The image and pre-image of a rotated object have some interesting mathematical properties.
The following are the three basic properties of rotations :
1. A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
2. A rotation preserves lengths of segments.
3. A rotation preserves measures of angles.
When parallel lines are rotated, their images are also parallel. A line is only parallel to itself when rotated exactly 180°.
Example 1 :
The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° counterclockwise about the origin and determine whether image and pre-image of the rotated object satisfy the properties.
Answer :
Step 1 :
Trace triangle xyz and the x- and y-axes onto a piece of paper.
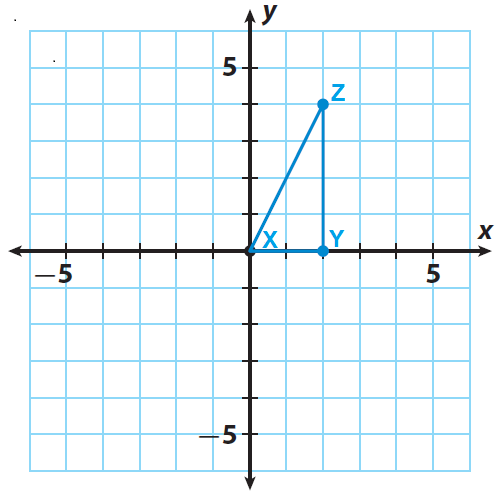
Step 2 :
Rotate your triangle 90° counterclockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.
Step 3 :
Sketch the image of the rotation. Label the images of points X, Y, and Z as X', Y', and Z'.
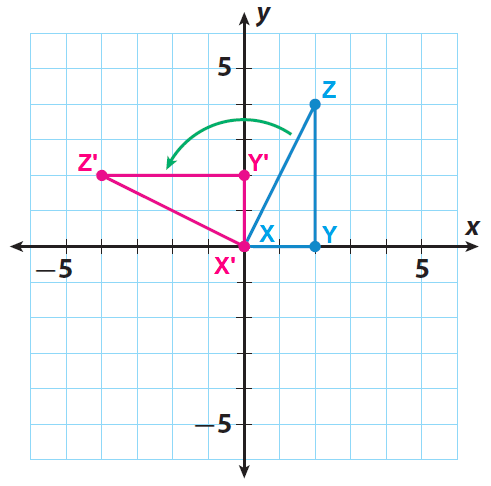
Step 4 :
The rotation done above maps each side to its corresponding side and each angle to its corresponding angle. And also, the rotation preserves lengths of segments and measures of angles. So, the rotation done above satisfies the properties.
Example 2 :
The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° clockwise about the origin and determine whether image and pre-image of the rotated object satisfy the properties.
Answer :
Step 1 :
Trace triangle xyz and the x- and y-axes onto a piece of paper.
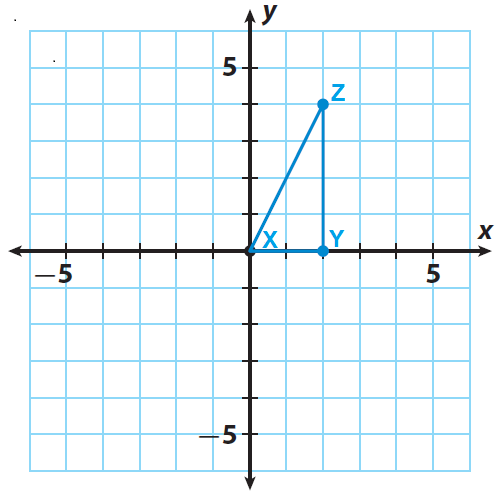
Step 2 :
Rotate your triangle 90° clockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.
Step 3 :
Sketch the image of the rotation. Label the images of points X, Y, and Z as X", Y", and Z".
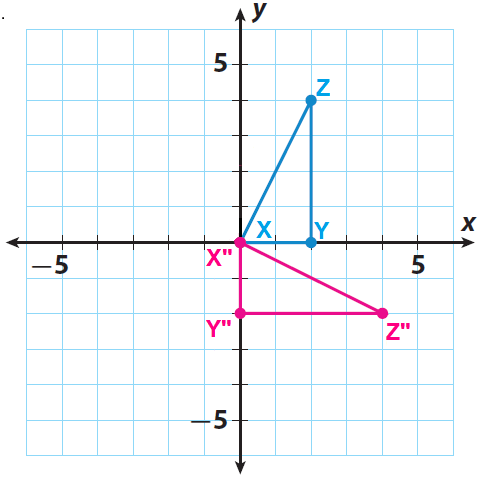
Step 4 :
The rotation done above maps each side to its corresponding side and each angle to its corresponding angle. And also, the rotation preserves lengths of segments and measures of angles. So, the rotation done above satisfies the properties.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
