PROPERTIES OF RATIO AND PROPORTION

Properties of Ratio

Property 1 :

Ratio exists only between quantities of the same kind.

Property 2 :

Quantities to be compared (by division) must be in the same units.

Property 3 :

The order of the terms in a ratio is important.

Property 4 :

Both terms of a ratio can be multiplied or divided by the same (non–zero) number. Usually a ratio is expressed in lowest terms (or simplest form).

Property 5 :

The order of the terms in a ratio is important.

Property 6 :

To compare two ratios, convert them into equivalent like fractions.

Property 7 :

If a quantity increases or decreases in the ratio a : b, then new quantity is

= (b x original quantity)/a

The fraction by which the original quantity is multiplied to get a new quantity is called the factor multiplying ratio.

Property 8 :

One ratio is the inverse of another, if their product is 1. Thus a : b is the inverse of b : a and vice–versa.

Property 9 :

A ratio a : b is said to be of greater inequality if a > b and of less inequality if a < b.

Property 10 :

The ratio compounded of the two ratios a : b and c : d is ac : bd.

Property 11 :

A ratio compounded of itself is called its duplicate ratio.

Thus a² : b² is the duplicate ratio of a : b. Similarly, the triplicate ratio of a : b is a³ : b³.

Property 12 :

The sub–duplicate ratio of a : b is √a : √b and the sub triplicate ratio of a : b is ³√a : ³√b.

Property 13 :

If the ratio of two similar quantities can be expressed as a ratio of two integers, the quantities are said to be commensurable; otherwise, they are said to be in-commensurable.

Property 14 :

√3 : √2 cannot be expressed as the ratio of two integers and therefore, √3 and √2 are in-commensurable quantities.

Property 15 :

Continued Ratio is the relation (or compassion) between the magnitudes of three or more quantities of the same kind. The continued ratio of three similar quantities a, b, c is written as a : b : c.

Properties of Proportion

Property 1 :

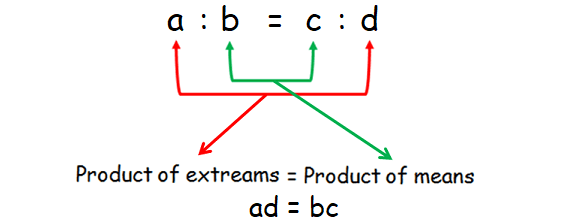
Consider the following proportion :

a : b = c : d

a and d ----> extremes

b and c ----> means

In a proportion,

product of extremes = product of means

In the proportion a : b = c : d, we have

ad  =  bc

This property is called cross product rule.

Property 2 :

Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion.

If three quantities a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.

Since three quantities a, b, c are in continuous proportion, we can write them as

a : b = b : c

Using cross product rule, we can solve for the mean proportion b.

product of means = product of extremes

b² = ac

Taking square root on both sides,

b = √ac

Property 3 :

In a proportion a : b = c : d, all the four quantities need not be of the same type. The first two quantities should be of the same kind and last two quantities should be of the same kind.

Property 4 :

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

Then their inverse ratios will also be in proportion.

b : a = d : c

This property is called invertendo.

Property 5 :

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

By interchanging the means b and c, we get two new ratios:

a : c and b : d

Now, the two ratios a : c and b : c are in proportion.

a : c = b : d

This property is called alternendo.

Property 6 :

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, by adding the second term to the first term, we get 

(a + b) : b and (c + d) : d

Now, the two ratios (a + b) : b and (c + d) : d are in proportion.

(a + b) : b = (c + d) : d

This property is called componendo.

Property 7 :

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, by subtracting the second term from the first term, we get 

(a - b) : b and (c - d) : d

Now, the two ratios (a - b) : b and (c - d) : d are in proportion.

(a - b) : b = (c - d) : d

This property is called dividendo.

Property 8 :

Let the two ratios a : b and c : d be in proportion.

a : b = c : d

In each ratio, add the second term to the first term and take the result as the first term, subtract the second term from the first term and take the result as the second term.

Then, we have

(a + b) : (a - b)

(c + d) : (c - d)

Now, the above two ratios are in proportion.

(a + b) : (a - b) = (c + d) : (c - d)

This property is called componendo and dividendo.

Property 9 :

Consider the following continued proportion.

a : b = c : d = e : f =..........

Add all the first terms and take the result as the first term and add all the second terms and take the result as the second term.

Then, we get

(a + c + e + ........) : (b + d + f + ........)

Now, the ratio (a + c + e + ........) : (b + d + f + ........) is equal to each ratio in the above continued proportion.

That is,

a : b = c : d = e : f =..... = (a + c + e + .....) : (b + d + f + .....)

This property is called addendo.

Property 10 :

Consider the following continued proportion.

a : b = c : d = e : f =..........

Subtract all the first terms (except the first term in the first ratio 'a') from the first term of the first ratio and  take the result as the first term and subtract all the second terms (except the second term in the first ratio 'b') from the second term of the first ratio and  take the result as the second term.

Then, we get

(a - c - e - ........) : (b - d - f - ........)

Now, the ratio (a - c - e + ........) : (b - d - f - ........) is equal to each ratio in the above continued proportion.

That is,

a : b = c : d = e : f =..... = (a - c - e - .....) : (b - d - f - .....)

This property is called subtrahendo.

Video Lessons

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.