PROPERTIES OF RADICALS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. Simplify : √6 ⋅ √15
2. Simplify : √35 ÷ √7
3. Simplify : 3√425 + 4√68
4. Simplify : √243 - 5√12 + √27
5. Simplify : √4 + 3√27 + 4√64
6. Simplify : 3√4 ⋅ 3√16
7. If √y = 1/5, then find the value of y.
8. Solve for x : 2√x - 2 = 10.
9. If 3√a = 1/2, then find the value of a.
10. If (3√8)7 ⋅ (√2)-4 = 2k, then solve for k.
11. Evaluate √(41 - (√21 + (√(19 - √9)))
12. The square root of 2722 - 1282 is
a) 144 b) 200 c) 240 d) 256
13. How many two digit numbers satisfy this property : The unit digit of the square of the two digit number is 8 ?
a) 1 b) 2 c) 3 d) none
14. If 52/x = √(169/289), the value of x is :
a) 52 b) 58 c) 62 d) 68
15. If 0.13 + p2 = 13, then p equals
a) 0.01 b) 0.1 c) 10 d) 100
16. √x / √441 = 0.02, then the value of x is
a) 0.1764 b) 1.764 c) 1.64 d) 2.64
17. If √(x - 1)(y + 2) = 7, x and y being positive whole numbers, then the values of x and y respectively are
a) 8, 5 b) 15, 12 c) 22, 19 d) none
18. If √(0.04 x 4 x a) = 0.004 x 0.4 x √b, then a/b is
a) 16 x 10-3 b) 16 x 10-4 c) 16 x 10-5 d) 16 x 10-6

1. Answer :
= √6 ⋅ √15
= √(6 ⋅ 15)
= √(2 ⋅ 3 ⋅ 3 ⋅ 5)
= 3√(2 ⋅ 5)
= 3√10
2. Answer :
= √35 ÷ √7
= √(35/7)
= √5
3. Answer :
Decompose 425 and 68 into prime factors using synthetic division.
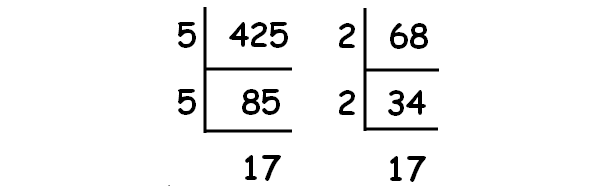
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
3√425 + 4√68 :
= 3(5√17) + 4(2√17)
= 15√17 + 8√17
= 23√17
4. Answer :
Decompose 243, 12 and 27 into prime factors using synthetic division.
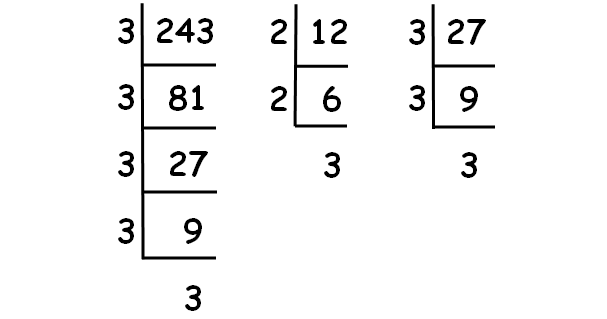
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
5. Answer :
√4 = √(2 ⋅ 2) = 2
3√27 = 3√(3 ⋅ 3 ⋅ 3) = 3
4√625 = 4√(5 ⋅ 5 ⋅ 5 ⋅ 5) = 5
√4 + 3√27 + + 4√64 :
= 2 + 3 + 5
= 10
6. Answer :
= 3√4 ⋅ 3√16
= 3√(4 ⋅ 16)
= 3√(4 ⋅ 4 ⋅ 4)
= 4
7. Answer :
√y = 1/5
y = (1/5)2
y = 12/52
y = 1/25
8. Answer :
2√x - 2 = 10
2√x = 12
√x = 6
x = 62
x = 36
9. Answer :
3√a = 1/2
a = (1/2)3
a = 13/23
a = 1/8
10. Answer :
(3√8)7 ⋅ (√2)-4 = 2k
27 ⋅ (21/2)-4 = 2k
27 ⋅ 2-2 = 2k
27 - 2 = 2k
25 = 2k
k = 5
11. Answer :
√(41 - (√21 + (√(19 - √9)))
Considering the quantity inside the most interior bracket.
(√(19 - √9)) = (√(19 - √(3⋅3))
= (√(19 - 3))
= √16
= √4 ⋅ 4
= 4
12. Answer :
= √(2722 - 1282)
Using algebraic identity a2 - b2, we get
= (a + b) (a - b)
= √(272 + 128) (272 - 128)
= √400 (144)
= √20(20) ⋅ 12 ⋅ 12
= 20 ⋅ 12
= 240
So, option c is correct.
13. Answer :
We should get 8, by multiplying a number by a same number. It is not true, because multiplying 2 and 4 or multiplying 1 and 8 only we will receive 8.
Then, the answer is none (option d)
14. Answer :
52/x = √(169/289)
52/x = √(13 ⋅ 13)/(17 ⋅ 17)
52/x = 13/17
Doing cross multiplication, we get
52(17) = 13 x
x = 52(17)/13
x = 4(17)
x = 68
15. Answer :
If 0.13 / p2 = 13, then p equals
0.13 / p2 = 13
0.13/13 = p2
p2 = 13/1300
p2 = 1/100
p = √(1/100)
p = 1/10
p = 0.1
So, option b is correct.
16. Answer :
√x / √441 = 0.02
√x / √(21 ⋅21) = 0.02
√x/21 = 0.02
√x = 0.02(21)
√x = 0.42
x = (0.42)2
x = 0.1764
So, the answer is option a.
17. Answer :
Given that,
√(x - 1)(y + 2) = 7
Option a :
x = 8 and y = 5
√(x - 1)(y + 2) = √(8 - 1)(5 + 2)
= √7(7)
= 7
So, option a is correct. The value of x is 8 and y is 5.
18. Answer :
√(0.04 x 4 x a) = 0.004 x 0.4 x √b
Squaring both sides, we get
(0.04 x 4 x a) = (0.004 x 0.4 x √b)2
(0.04 x 4 x a) = (0.004 x 0.4 x √b)2
(0.04 x 4 x a) = (0.004)2 x (0.4)2 x b
a/b = (0.004)2 x (0.4)2 / (0.04 x 4 x a)
a/b = (0.000016 x 0.16) / (0.04 x 4)
a/b = (0.000016 x 0.16) / (0.04 x 4)
= 0.000016
a/b = 16 x 10-6
So, option d is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

