PROPERTIES OF DETERMINANTS

Property 1 :

The determinant of a matrix remains unaltered if its rows are changed into columns and columns into rows.

|A| = |A^T|

Since the row-wise expansion is same as the column-wise expansion, the result holds good.

Property 2 :

If any two rows / columns of a determinant are interchanged, then the determinant changes in sign but its absolute value remains unaltered.

Verification :

Consider a determinant |A| shown below. 

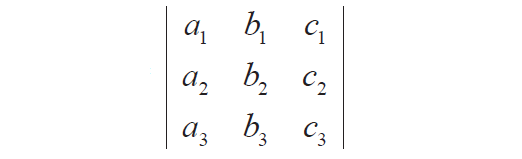
|A| = a₁(b₂c₃ - b₃c₂) - b₁(a₂c₃ - a₃c₂) + c₁(a₂b₃ - a₃b₂)

Consider a determinant |A₁| shown below by interchanging the second and third rows in the determinant |A| above.  

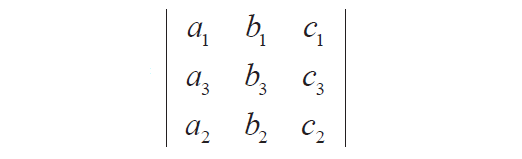
|A₁| = a₁(b₃c₂ - b₂c₃) - b₁(a₃c₂ - a₂c₃) + c₁( a₃b₂ - a₂b₃)

= -[a₁(b₂c₃ - b₃c₂) - b₁(a₂c₃ - a₃c₂) + c₁(a₂b₃ - a₃b₂)]

= -|A|

Therefore |A| = |-A₁|. Thus the property is verified.

Property 3 : 

If there are n interchanges of rows (columns) of a matrix A then the determinant of the resulting matrix is

(- 1)ⁿ|A|

Property 4 : 

If two rows (columns) of a matrix are identical, then its determinant is zero.

Verification :

Consider a determinant |A| shown below with 2^nd and 3^rd rows are identical. 

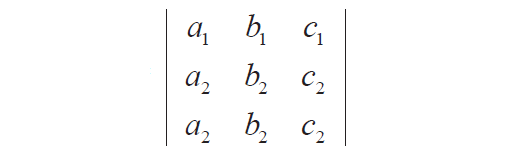
|A| = a₁(b₂c₂ - b₂c₂) - b₁(a₂c₂ - a₂c₂) + c₁(a₂b₂ - a₂b₂)

= 0

Thus, the property is verified.

Property 5 : 

If a row (column) of a matrix A is a scalar multiple of another row (or column) of A, then its determinant is zero.

Note :

(i) If all entries of a row or a column are zero, then the determinant is zero.

(ii) The determinant of a triangular matrix is obtained by the product of the principal diagonal elements.

Property 6 :

If each element in a row (or column) of a matrix is multiplied by a scalar k, then the determinant is multiplied by the same scalar k.

Verification : 

Consider a determinant |A| shown below. 

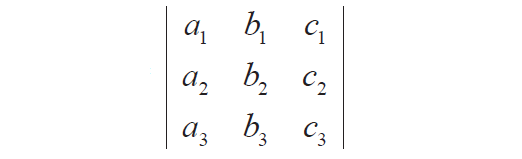
 |A| = a₁(b₂c₃ - b₃c₂) - b₁(a₂c₃ - a₃c₂) + c₁(a₂b₃ - a₃b₂)

Consider a determinant |A₁| shown below by multiplying the first row of the determinant |A| above by the constant k, where k ≠ 0. 

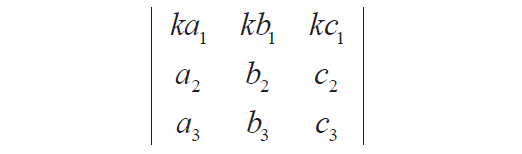
|A₁| = ka₁(b₂c₃- b₃c₂) - kb₁(a₂c₃ - a₃c₂) + kc₁(a₂b₃ - a₃b₂)

  = k[a₁(b₂c₃ - b₃c₂) - kb₁(a₂c₃ - a₃c₂) + kc₁(a₂b₃ - a₃b₂)]

|A₁| = K|A|

Thus, the property is verified. 

Note : 

If A is a square matrix of order n, then

(i) |AB| = |A||B|

(ii) If AB = O then either |A| = 0 or |B| = 0.

(iii) |Aⁿ|= (|A|)ⁿ

Property 7 : 

If each element of a row (or column) of a determinant is expressed as sum of two or more terms then the whole determinant is expressed as sum of two or more determinants. 

The above property is illustrated below with three determinants |A|, |B| and |C|. 

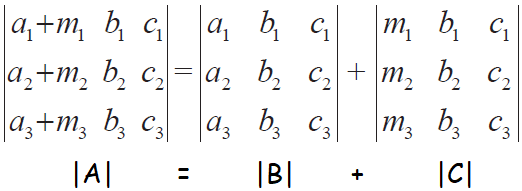
Verification :

By taking first column expansion it can be verified easily.

|A| = (a₁ + m₁)(b₂c₃ - b3c₂) - (a₂ + m₂)(b₁c₃ - b₃c₁) + (a₃ + m₃)(b₁c₂-b₂c₁)

= a₁(b₂c₃ - b3c₂) - a₂(b₁c₃ - b₃c₁) + a₃(b₁c₂-b₂c₁) + m₁(b₂c₃ - b3c₂) - m₂(b₁c₃ - b₃c₁) + m₃(b₁c₂-b₂c₁) ----(1)

|B| = a₁(b₂c₃ - b₃c₂) - b₁(a₂c₃ - a₃c₂) + c₁(a₂b₃ - a₃b₂)

|C| = m₁(b₂c₃ - b₃c₂) - m₂(b₁c₃ - b₃c₁) + m₃(b₁c₂ - b₂c₁)

|B| + |C| = a₁(b₂c₃ - b3c₂) - a₂(b₁c₃ - b₃c₁) + a₃(b₁c₂-b₂c₁) + m₁(b₂c₃ - b3c₂) - m₂(b₁c₃ - b₃c₁) + m₃(b₁c₂-b₂c₁) ----(2)

From (1) and (2), 

|A| = |B| + |C|

Thus, the property is verified. 

Property 8 : 

If, to each element of any row (column) of a determinant the equi-multiples of the corresponding entries of one or more rows (columns) are added or subtracted, then the value of the determinant remains unchanged.

Verification :

Consider a determinant |A| shown below. 

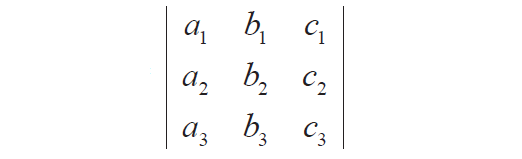
Consider another determinant |A₁| shown below. 

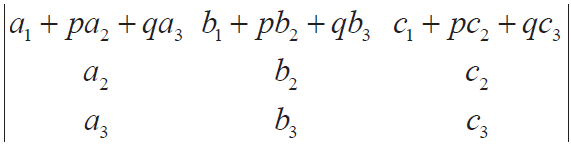
Using Property 7 in the above determinant |A₁|,

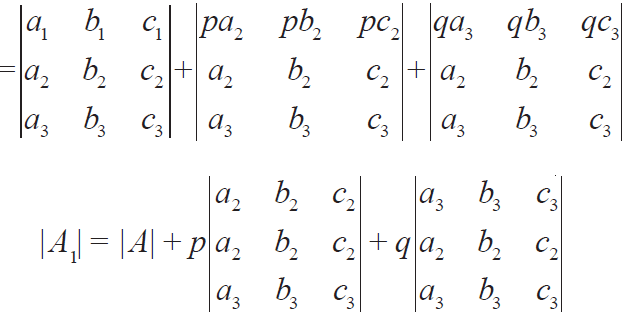
 |A₁| = |A| + p(0) + q(0) = |A| (using Property 4)

Therefore |A₁| = |A|

This property is independent of any fixed row or column.

Apart from if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.