PROPERTIES OF CUBE NUMBERS

We know that the word 'Cube' is used in geometry. A cube is a solid figure which has all its sides are equal.

If the side of a cube in the adjoining figure is ‘a’ units then its volume is given by

= a ⋅ a ⋅ a

= a³ cubic units.

Here a³ is called 'a cubed' or 'a raised to the power 3' or 'a to the power 3'.

Now, consider the number 1, 8, 27, 64, 125,....... 

These are called perfect cubes or cube numbers.

Each of them is obtained when a number is multiplied by itself three times.

Examples :

1 ⋅ 1 ⋅ 1  =  1³

2 ⋅ 2 ⋅ 2  =  2³

3 ⋅ 3 ⋅ 3  =  3³

5 ⋅ 5 ⋅ 5  =  5³

The following are the cubes of numbers from 11 to 20.

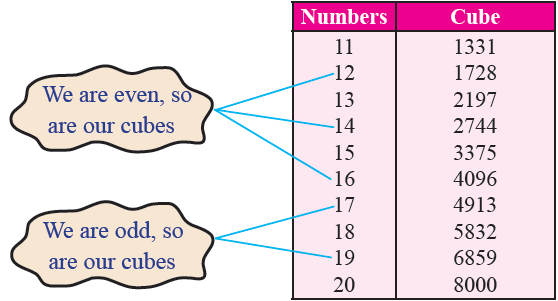
From the above table we observe the following properties of cubes :

Property 1 : 

For numbers with their unit’s digit as 1, their cubes also will have the unit’s digit as 1.

For example,

1³ = 1

11³ = 1331

21³ = 9261

31³ = 29791

Property 2 :

The cubes of the numbers with 1, 4, 5, 6, 9 and 0 as unit digits will have the same unit digits.

For example, 

14³ = 2744

15³ = 3375

16³ = 4096

20³ = 8000

Property 3 :

The cube of numbers ending in unit digit 2 will have a unit digit 8 and the cube of the numbers ending in unit digit 8 will have a unit digit 2.

For example, 

12³ = 1728

18³ = 5832

Property 4 :

The cube of the numbers with unit digits as 3 will have a unit digit 7 and the cube of numbers with unit digit 7 will have a unit digit 3.

For example, 

13³ = 2197

27³ = 19683

Property 5 :

The cubes of even numbers are all even; and the cubes of odd numbers are all odd.

For example, 

18³ = 5832 (even)

27³ = 19683 (odd) 

Property 6 :

The sum of the cubes of first n natural numbers is equal to the square of their sum. 

1³ + 2³ + 3³ + ....... + n³ = (1 + 2 + 3 + ..... + n)²

For example,

1³ + 2³ + 3³ + 4³ = (1 + 2 + 3 + 4)²

1 + 8 + 27 + 64 = 10²

100 = 100

 Practice Questions

Problem 1 :

Is 64 a perfect cube ?

Solution : 

Using prime factorization, we can write 64 as given below.

64 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

64 = 2³ ⋅ 2³ = (2 ⋅ 2)³ = 4³

Hence, 64 is a perfect cube. 

Problem 2 :

Is 500 a perfect cube ?

Solution : 

Using prime factorization, we can write 500 as given below.

500 = 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5

There are three 5’s in the product but only two 2’s.

Hence, 500 is not a perfect cube. 

Problem 1 :

The cube root of 0.000216 is

a)  0.6    b)  0.06    c) 0.006     d) none

Solution :

= ∛0.000216

= ∛(216/1000000)

= ∛(6 x 6 x 6) / (100 x 100 x 100)

= 6/100

= 0.06

So, option b is correct.

Problem 2 :

 ∛(4  12/125) = ?

a)  1  2/5    b)  1  3/5    c) 1  4/5     d) 2  2/5

Solution :

=  ∛(4  12/125)

Converting the mixed fraction as improper fraction, we get

= ∛(4 x 125 + 12)/125

= ∛(500 + 12)/125

= ∛512/125

= = ∛(8 x 8 x 8)/(5 x 5 x 5)

= 8/5

Converting improper fraction, we get

= 1  3/5

So, option b is correct.

Problem 3 :

 ∛(√0.000064) = ?

a)  0.02     b)  0.2   c) 2     d) None

Solution :

=  ∛(√0.000064)

First we will try to remove the square root.

=  ∛√(64/1000000)

=  ∛√(8 x 8)/(1000 x 1000)

When two same values are multiplied, we may take one value out of the square root.

= ∛8/1000

= ∛(2 x 2 x 2)/(10 x 10 x 10)

= 2/10

= 0.2

Problem 4 :

The largest four digit number which is perfect cube is 

a)  8000     b)  9261   c) 9999     d) None

Solution :

Option a :

= ∛8000

= ∛2 x 2 x 2 x 10 x 10 x 10

= 2 x 10

= 20

Option b :

= ∛9261

= ∛3 x 3 x 3 x 7 x 7 x 7

= 3 x 7

= 21

Option c :

= ∛9999

= ∛3 x 3 x 1111

It is not a perfect cube.

So, option a is correct.

Problem 5 :

What is the smallest number by which 3600 be divided to make it a perfect cube. 

a)  9     b)  50   c) 300     d) 450

Solution :

= ∛3600

= ∛2 x 2 x 2 x (2 x 5 x 5 x 3 x 3)

(2 x 5 x 5 x 3 x 3) is the number to be divided to make it as perfect cube.

So, 450 is the number to be removed to make it as perfect cube.

Problem 6 :

A rectangular solid has a length three times the width and a height twice its width. If the volume of the rectangle solid is 384 𝑖𝑛³, determine the dimensions of the rectangular solid.

Solution :

Let x be the width

length = 3x

height = 2x

Volume of rectangular prism = length x width x height

x (3x)(2x) = 384 𝑖𝑛³

6x³ = 384

x³ = 384/6

x³ = 64

x = ∛64

x = ∛(4 x 4 x 4)

x = 4

length = 3x ==> 12 cm

width = 4 cm

height = 2x ==> 8 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.