PROBLEMS ON VOLUME
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find volume of the shapes, we will be using the formulas given below.
Volume of sphere = (4/3) π r3
Volume of hemisphere = (2/3) π r3
Volume of cone = (1/3) π r2h
Volume of cylinder = π r2h
Problem 1 :
A steel bar is 2.2 m long and has a diameter of 5 cm. Find the volume of the bar in cm3.
Solution :
Length of steel bar = 2.2 m (or) 220 cm
Radius = 5/2 ==> 2.5 cm
Volume of steel bar = π r2h
= (3.14) (2.5)2(220)
= 4317.5 cm3
Problem 2 :
A stainless steel wine vat is cylindrical with base diameter 1.8 m and height 6 m. How much wine does it hold if it is 90% full?
Solution :
Radius = 1.8 m, height = 6 m
Volume of steel bar = 90% of π r2h
= 0.90 x 3.14 x (1.8)2 x 6
= 54.93 m3
Problem 3 :
A box has a square base and its height is 12 cm. If the volume of the box is 867 cm3, find its length.
Solution :
Let base length of the square as x.
Volume of box = 867 cm3
Area of square base x height = 867
x2 x 12 = 867
x2 = 867/12
x2 = 72.25
x = 8.5 cm
Problem 4 :
15.4 mm of a rain falls on a rectangular shed roof of length 12 m and width 5.5 m. All of the water goes into a cylindrical tank of base diameter 4.35 m. By how much does the water level in the tank rise in mm ?
Solution :
Measures of rectangular shed :
Length = 12 m = 12000 mm
width = 5.5 m = 5500 mm
height = 15.4 mm
Radius = 4.35/2 = 2.175 m
= 2175 mm
Volume of water in rectangular tank = Volume of water in cylindrical tank
length x width x height = π r2h
12000 x 5500 x 15.4 = 3.14 x (2.175)2 x h
h = (12000 x 5500 x 15.4)/3.14 x (2175)2
h = 68.42 mm
Problem 5 :
Find the volume of the figure shown below.
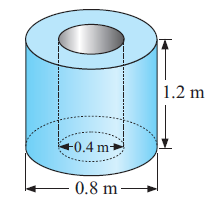
Solution :
Volume = Base area x height
Base area = Area of large circle - Area of small circle
Let R and r be radius of large and small circles respectively.
R = 0.8/2, r = 0.4/2
R = 0.4 m and r = 0.2 m
Area of base = πR2 - πr2
= π(0.42 - 0.22)
= 3.14(0.12)
Area of base = 0.3768 m2
Height = 1.2 m
Volume = 0.3768 x 1.2
= 0.45216 m3
Problem 6 :
Find the volume of the figure given below.
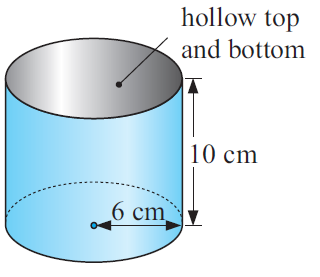
Solution :
Volume of cylinder = πr2h
radius = 6 cm and height = 10 cm
= π(6)2 (10)
= 3.14(36)(10)
Volume of cylinder = 1130.4 cm3
Problem 7 :
Tom has just had a load of sand delivered. A pile of sand is in the shape of a cone of radius 1.6 m and height 1.2 m. Find the volume of sand Tom has had delivered.
Solution :
Volume of sand to be delivered = (1/3) πr2h
radius = 1.6 m and height = 1.2 m
= (1/3) π(1.6)2(1.2)
= (1/3)x3.14x(1.6)2(1.2)
= 3.19 m3
Volume of sand delivered is 3.19 m3.
Problem 8 :
A cylinder of radius 12 cm contains water to a depth of 20cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. find the radius of the ball.
Solution :
Radius of cylinder = 12 cm
height = 6.75 cm
Volume of sphere = (4/3) πr3
Volume of sphere = volume of water raises in the cylinder
(4/3) πr3 = πr2h
(4/3) r3 = 122(6.75)
r3 = 144 x 6.75 x (3/4)
r3 = 729
r = 8 cm
So, the radius of the sphere is 8 cm.
Problem 9 :
The height of a right circular cylinder is equal to its diameter, if it is melted and recast into a sphere of radius equal to the radius of the cylinder; find the volume of unused material.
Solution :
Diameter = height
2r = h
r = h/2
Radius of sphere = radius of cylinder = h/2
Volume of cylinder = πr2h
= π(h/2)2h
= (1/4) πh3 -----(1)
Volume of sphere = (4/3)πr3
= (4/3)π(h/2)3
= (4/3) (πh3/8)
= (1/6)πh3
Difference = (1/4) πh3 - (1/6)πh3
= (1/12) πh3
= (1/3) π(h2/4)h
= (1/3) (1/4) πh3
So, 1/3 of the material has not used.
Problem 10 :
What is the capacity of a cylinder having radius 0.5cm and height 0.4 cm ?
Solution :
Radius = 0.5 cm
Height = 0.4 cm
Capacity of the cylinder = volume of cylinder
= πr2h
= π(0.5)2(0.4)
= 0.1π
= 0.1 x 3.14
= 0.314 cm3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problems on Exponents and Radicals
Feb 21, 26 08:28 PM
SAT Math Problems on Exponents and Radicals -
SAT Math Problems on Angles
Feb 21, 26 08:20 PM
SAT Math Problems on Angles -
Digital SAT Math Problems and Solutions (Part - 9)
Feb 21, 26 10:41 AM
Digital SAT Math Problems and Solutions (Part - 9)

