PROBLEMS ON VOLUME

Problem 1 :

A steel bar is 2.2 m long and has a diameter of 5 cm. Find the volume of the bar in cm³.

Solution :

Length of steel bar  =  2.2 m  (or)  220 cm

Radius  =  5/2  ==>  2.5 cm

Volume of steel bar  =  π r²h

=  (3.14) (2.5)²(220)

=  4317.5 cm³

Problem 2 :

A stainless steel wine vat is cylindrical with base diameter 1.8 m and height 6 m. How much wine does it hold if it is 90% full?

Solution :

Radius  =  1.8 m, height  =  6 m

Volume of steel bar  =  90% of π r²h

=  0.90 x 3.14 x (1.8)² x 6

=  54.93 m³

Problem 3 :

A box has a square base and its height is 12 cm. If the volume of the box is 867 cm³, find its length.

Solution :

Let base length of the square as x.

Volume of box  =  867 cm³

Area of square base x height  =  867

x² x 12  =  867

x²  =  867/12

x²  =  72.25

x  =  8.5 cm

Problem 4 :

15.4 mm of a rain falls on a rectangular shed roof of length 12 m and width 5.5 m. All of the water goes into a cylindrical tank of base diameter 4.35 m. By how much does the water level in the tank rise in mm ?

Solution :

Measures of rectangular shed :

Length  =  12 m  =  12000 mm

width  =  5.5 m  =  5500  mm

height  =  15.4 mm

Radius  =  4.35/2  =  2.175 m

=  2175 mm

Volume of water in rectangular tank  =  Volume of water in cylindrical tank

length x width x height  =  π r²h

12000 x 5500 x 15.4  =  3.14 x (2.175)² x h

h  =  (12000 x 5500 x 15.4)/3.14 x (2175)²

h  =  68.42 mm

Problem 5 :

Find the volume of the figure shown below.

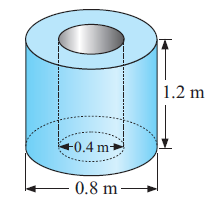
Solution :

Volume  =  Base area x height

Base area  =  Area of large circle - Area of small circle

Let R and r be radius of large and small circles respectively.

R  =  0.8/2, r  =  0.4/2

R  =  0.4 m and r  =  0.2 m

Area of base  =  πR² -  πr²

=   π(0.4² - 0.2²)

=  3.14(0.12)

Area of base  =  0.3768 m²

Height  =  1.2 m

Volume  =  0.3768 x 1.2

=  0.45216 m³

Problem 6 :

Find the volume of the figure given below.

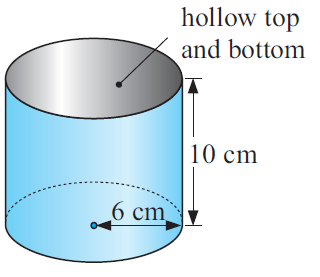
Solution :

Volume of cylinder  =  πr²h

radius  =  6 cm and height  =  10 cm

=  π(6)² (10)

=  3.14(36)(10)

Volume of cylinder  =  1130.4 cm³

Problem 7 :

Tom has just had a load of sand delivered. A pile of sand is in the shape of a cone of radius 1.6 m and height 1.2 m. Find the volume of sand Tom has had delivered.

Solution :

Volume of sand to be delivered  =  (1/3) πr²h

radius  =  1.6 m and height  =  1.2 m

=  (1/3) π(1.6)²(1.2)

=  (1/3)x3.14x(1.6)²(1.2)

=  3.19 m³

Volume of sand delivered is 3.19 m³_.

Problem 8 :

A cylinder of radius 12 cm contains water to a depth of 20cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. find the radius of the ball.

Solution :

Radius of cylinder = 12 cm

height = 6.75 cm

Volume of sphere = (4/3) πr³

Volume of sphere = volume of water raises in the cylinder

(4/3) πr³ = πr²h

(4/3) r³ = 12²(6.75)

r³ = 144 x 6.75 x (3/4)

r³ = 729

r = 8 cm

So, the radius of the sphere is 8 cm.

Problem 9 :

The height of a right circular cylinder is equal to its diameter, if it is melted and recast into a sphere of radius equal to the radius of the cylinder; find the volume of unused material.

Solution :

Diameter = height

2r = h

r = h/2

Radius of sphere = radius of cylinder = h/2

Volume of cylinder = πr²h

= π(h/2)²h

= (1/4) πh³ -----(1)

Volume of sphere = (4/3)πr³

= (4/3)π(h/2)³

= (4/3) (πh³/8)

= (1/6)πh³

Difference = (1/4) πh³ - (1/6)πh³

= (1/12) πh³

= (1/3) π(h²/4)h

= (1/3) (1/4) πh³

So, 1/3 of the material has not used.

Problem 10 :

What is the capacity of a cylinder having radius 0.5cm and height 0.4 cm ?

Solution :

Radius = 0.5 cm

Height = 0.4 cm

Capacity of the cylinder = volume of cylinder

= πr²h

= π(0.5)²(0.4)

= 0.1π

= 0.1 x 3.14

= 0.314 cm³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.