PROBLEMS ON VOLUME OF COMBINATION OF SOLIDS

Problem 1 :

A hollow cylindrical pipe is of length 40 cm. Its internal and external radii are 4 cm and 12 cm respectively. It is melted and cast into a solid cylinder of length 20 cm. Find the radius of the new solid.

Solution :

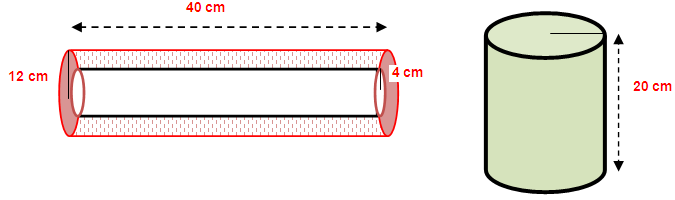
length of cylindrical pipe (h) = 40 cm

internal radius of the pipe (r) = 4 cm

external radius of the pipe (R) = 12 cm

Height of cylinder = 20 cm

Volume of hollow cylindrical pipe = Volume of cylinder

Π h (R² - r²) =  Π r² h

h (R² - r²)  =   r² h

(40) (12² - 4²)  =  r² (20)

(40) (144 - 16) =  r² (20)

(40) (128)/20  =  r²

r²  =  (40) (128)/20

r²  =  2 (128)

r  =  √256

r  =  16 cm

Therefore radius of cylinder  =  16 cm

Problem 2 :

An iron right circular cone of diameter 8 cm and height 12 cm is melted and recast into spherical lead shots each of radius 4 mm. How many lead shots can be made?

Solution :

diameter of right circular cone = 8 cm

radius of right circular cone (r) = 4 cm

Height of right circular cone (h) = 12 cm

Radius of spherical lead shot (r) = 4 mm

10 mm  =  1 cm

4 mm  =  (4/10) cm 

Volume of right circular cone

= n x (Number of spherical lead shots)

n  =  Volume of cone/Number of spherical lead shots

n  =   (1/3)Π r² h/(4/3)Π r³

n  =  (1/3) (4)² (12) x (3/4) (10/4)³

n =  3 x 5 x 5 x 10

n = 750 lead shots

Therefore 750 lead shots can be made.

Problem 3 :

A container with a rectangular base of length 4.4 m and breadth 2 m is used to collect rain water. The height of the water level in the container is 4 cm and water is transferred into a cylindrical vessel with radius 40 cm. What will be the height of the water level in the cylinder?

Solution :

Volume of water in cuboidal container  =  Volume of water in cylindrical container

lwh  =  Π r²h

l  =  4.4 m, w  =  2 m, h  =  4 cm ==>  4/100 ==>  1/25 m

r  =  40 cm ==>  40/100

4.4(2) (1/25)  =  Π (2/5)²h

h  =  4.4 (2) (1/25) (1/Π) (25/4)

h  =  2.2/Π

h  =  0.7 m

Problem 4 :

A cylindrical bucket of height 32 cm and radius 18 cm is filled with sand. The bucket is emptied on the ground and a conical heap and sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Solution :

Volume of sand in the cylindrical bucket  =  Volume of sand of conical heap

Let r₁, h₁ be the radius and height of cylindrical tank

Let r₂, h₂ be the radius and height of conical tank

Π r₁²h₁  =  (1/3)Π r₂²h₂

r₁  =  18 cm,  h₁  =  32 cm and h₂  =  24 cm

18²(32)  =  (1/3) r₂²(24)

18²(32)  =  8 r₂²

r₂² =  (18⋅18⋅32)/8

r₂  =  18(2)

r₂  =  36 cm

So, the radius of the conical heap is 36 cm.

Problem 5 :

A bucket of height 8 cm and made up of copper sheet is in the form of a frustum of a right circular cone with radii of its lower and upper ends as 3 cm and 9 cm respectively. Calculate :

(i) the height of the cone of which the bucket is a part.

(ii) the volume of water which can be filled in the bucket.

(iii) the area of copper sheet required to make the bucket. (Leave the answer in terms of Π)

Solution :

(i) the height of the cone = R + r

= 9 + 3

= 12 cm

(ii) Volume of frustum cone = (1/3) Πh(R² + r² + Rr)

h = 8 cm, R = 9 cm and r = 3 cm

= (1/3) Π x 8 (9² + 3² + 9(3))

= (1/3) Π x 8 (81 + 9 + 27)

= (1/3) Π x 8 (117)

= 39 x 8 Π

= 312 Π cm³

(iii) To find area of copper sheet required to make the bucket, we have to find the surface area 

= Πl(R + r)

Slant height = l = √h² + (R - r)²

l = √8² + (9-3)²

= √64 + 36

= √100

= 10

= Π x 10 (9 + 3)

= 120Π

Problem 6 :

The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in liters and the amount of sheet required to make this bucket and its cost at $2 per sq. dm of sheet.

Solution :

Height = 30 cm, R = 21 cm and r = 7 cm

 Volume of frustum cone = (1/3) Πh(R² + r² + Rr)

= (1/3) Π x 30(21² + 7² + 21(7))

= (1/3) Π x 30(441 + 49 + 147)

= 3.14 x 10(637)

= 20001.8 cm³

1 liter = 1000 cm³

= 20001.8/1000

= 20.02 liter

Slant height of the bucket, l = √h² + (R - r)²

l = √30² +(21 -7)²

l = √900 + 14²  = √900 + 196 = √1096

l = 33.1 cm

Total area of the metal sheet required to  make the bucket = πl(R + r) + πr²

= π× 33.1 (21 + 7) + π ×7²

= π × 33.1 × 28  + π × 49

= π × 926.8 + 49π

= π(926.8 + 49)

= 22/7 × 975.8

= 22 × 139.4

= 3,066.8 ≈ 3067 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.