PROBLEMS ON TRIANGLE IN TRIGONOMETRY FOR CLASS 11

Problem 1 :

In any triangle ABC, prove that the area triangle is

b² + c² − a²/4 cotA

Solution :

Cosine formula :

cos A  =  (b² + c² - a²) / 2bc

Given that :

=  b² + c² − a²/4 (cos A/sin A)

=  (b² + c² − a²) sin A/4 cos A  ---(1)

From cosine formula, we have

2bc cos A  =  b² + c² - a²

By applying the value of b² + c² - a² in (1)

  =  (2bc cos A) sin A/4 cos A

  =  (bc sin A)/2

  =  (1/2) bc sin A

  =  Area of triangle

Hence proved.

Problem 2 :

In a triangle ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm.

Solution :

Area of triangle  =  (1/2) ab sin C

  =  (1/2) 12(8) sin 30°

  =  48 (1/2)

  =  24 square units.

Hence it is proved.

Problem 3 : 

In a triangle ABC, if a = 18 cm, b = 24 cm and c = 30 cm, then show that its area is 216 sq.cm.

Solution :

Since the length of all sides are different, we have to use heron's formula to find the area.

a = 18 cm, b = 24 cm and c = 30 cm

s  =  (a + b + c)/2

  =  (18 + 24 + 30)/2

  =  72/2

 s = 36

s - a = 36-18  =  18

s - b = 36-24  =  12

s - c = 36-30  =  6

Area of triangle  = √s(s-a)(s-b)(s-c)

  = √36(18)(12)(6)

  =  216 square units.

Hence it is proved.

Problem 4 :

Two soldiers A and B in two different underground bunkers on a straight road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5km apart, find the distance of the intruder from B.

Solution :

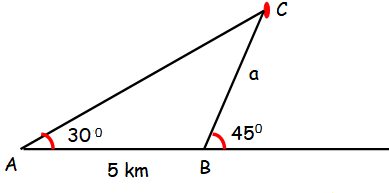
<A  =  30

<B + 45  =  180

<B  =  180 - 45  =  135

<A + <B  + <C  =  180

30 + 135 + <C  =  180

<C  =  180 - 165

<C  =  15

BC  =  a, AC  =  b and AB  =  c

Sine formula :

a/sin A  =  b/sin B  =  c/sin C

a/sin 30  =  b/sin 135  =  5/sin 15

 a/(1/2)  =  5/sin (45-30)

2a  =  5/sin (45-30)

sin (45-30) = sin 45 cos 30 - cos 45 sin 30

    =  (1/√2)(√3/2) -  (1/√2)(1/2)

   =  √3/2√2 - 1/2√2

   =  (√3 - 1)/2√2

2a  =  5/[(√3 - 1)/2√2]

2a  =  10√2/(√3 - 1)

a  =  5√2/(√3 - 1)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.