PROBLEMS ON SURFACE AREA OF CONE

Problem 1 :

If the vertical angle and the radius of the right circular cone are 60 degree and 15 cm respectively, then find its slant height and curved surface area.

Solution :

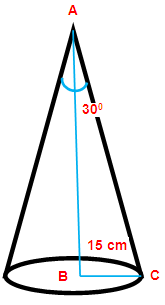
Vertical angle of the  right circular cone = 60°

radius of the cone (r) = 15 cm

In the triangle ABC, ∠ABC = 30°

 BC = 15 cm

Opposite side (BC) = 15 cm

Adjacent side (AB) = ?

Hypotenuse side (AC) = ?

here,  we need to find the measurement of the side AC. So we have to use sinθ.

sin θ = Opposite side/Hypotenuse side

sin 30° = BC/AC      

(1/2) = 15/AC

AC = 30 cm

Slant height (L) = 30 cm

Curved surface area of cylinder  =  π r l

=  π ⋅ 15 ⋅ 30 

=  450 π cm²

So, curved surface area of cone is 450 π cm²

Problem 2 :

If the circumference of the base of the solid right circular cone is 236 and its slant height is 12 cm, find its curved surface area.

Solution :

Circumference of the base  =  236 cm

Slant height (L)  =  12 cm

2 Π r  =  236

Πr  =  236/2

Π r  =  118

Curved surface area of cone  =  Π r l

=  118 (12) 

=  1416 cm²

So, curved surface area of cone is 1416 cm²

Problem 3 :

A heap of paddy is in the form of a cone whose diameter is 4.2 m and height is 2.8 m. If the heap is to be covered exactly by a canvas to protect it from rain, then find the area of the canvas needed.

Solution :

Diameter of heap of paddy  =  4.2 m

r  =  4.2/2

r  =  2.1 m

height of paddy (h) = 2.8 m

 l²  =  r²+h²

l  =  √(2.1)²+(2.8)² 

l  =  √(4.41+7.84)

l = √12.25

l = √(3.5 ⋅3.5)

l = 3.5 cm

Curved surface area of heap of paddy  =  Π r l

= (22/7) ⋅ 2.1 ⋅ 3.5

= 22 ⋅ 2.1 ⋅ 0.5

= 23.1 cm²

So, curved surface area of paddy is 23.1 cm².

Problem 4 :

The central angle and radius of a sector of a circular disc are 180 degree and 21 cm respectively. If the edges of the sector are joined together to make a hollow cone, then find the radius of the cone.

Solution :

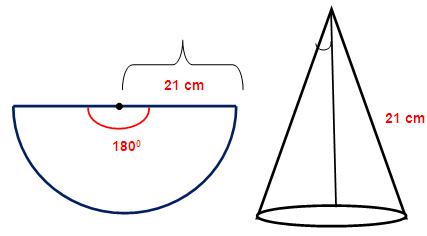
The cone is being created by joining the radius. So the radius of the sector is going to be the slant height of the cone.

Slant height L  =  21 cm

Arc length of the sector  =  Circumference of the base of the cone

 Length of arc = (θ/360) ⋅ 2Π R

Here R represents radius of the sector

=  (180/360)  ⋅ 2 ⋅ (22/7) ⋅ 21

=  (1/2) ⋅ 2 ⋅ 22 ⋅ 3

=  66 cm

So, circumference of the base of the cone = 66

2 Π r  =  66

2 ⋅ (22/7) ⋅ r = 66

r  =  10.5 cm

So, radius of the cone is 10.5 cm.

Problem 5 :

Radius and slant height of a solid right circular cone are in the ratio 3:5. If the curved surface area is 60Π cm², then find its radius and slant height.

Solution :

Radius and slant height of a solid right circular cone are in the ratio 3:5.

r : L  =  3 : 5 

r / L  =  3/5

r  =  3L/5

Curved surface area of cone  =  60 Πcm² 

Π r L  =  60Π

Π ⋅ (3L/5) ⋅ L  =  60Π

l²  =  60 Π ⋅ (1/Π) ⋅ (5/3)

l²  =  60 ⋅ (5/3)

l²  =  100

l  =  10 cm

r  =  3(10)/5

r  =  30/5

r  =  6 cm

So, radius and slant height of cone are 6 cm and 10 cm respectively.

Problem 6 :

A sector containing an angle of 120 degree is cut off from a circle of radius 21 cm and folded into a cone. Find the curved surface area of a cone.

Solution :

The cone is being created by joining the radius. So the radius of the sector is going to be the slant height of the cone.

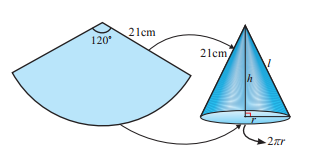
Slant height (l)  =  21 cm

Arc length of the sector  =  Circumference of the base of the cone

Length of arc  =  (θ/360) ⋅ 2Π R

Here R represents radius of the sector

=  (120/360) ⋅ 2 ⋅ (22/7) ⋅ 21

=  (1/3) ⋅ 2 ⋅ 22 ⋅ 3

=  44 cm

So, circumference of the base of the cone = 44

2Πr  =  44

2 ⋅ (22/7) ⋅ r  =  44

r   =  7 cm

Now, we need to find the curved surface area of cone 

Curved surface area of cone  =  Πrl

=  (22/7) x 7 x 21 

=  462 cm²

So, curved surface area is 462 cm². 

Problem 7 :

A cylinder, a cone and a sphere are of the same radius and same height. Find the ratio of their curved surface

Solution :

Curved surface area of cylinder = 2Πrh

Curved surface area of cone = Πrl

Curved surface area of sphere = 3Πr²

Ratio between curved surface area :

2 Πr h : Πrl : 3Πr²

Here r = h = l

2 Πr² : Πr² : 3Πr²

2 : 1 : 3

So, the required ratio is 2 : 1 : 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.