PROBLEMS ON SURFACE AREA OF COMBINED SHAPES
Problem 1 :
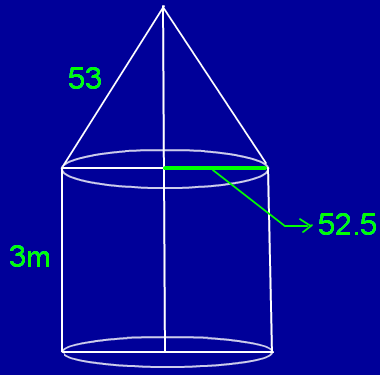
A circus tent is in the form of a cylinder with a height of 3 m and conical above it. If the base radius is 52.5 m and the slant height of the cone is 53 m, find the canvas needed to make the tent.
Solution :
Cylindrical part :
The radius of the cylindrical part (r) = 52.5 m
Height of the cylindrical part(h) = 3 m
Curved surface-area of the cylindrical part = 2πrh
= 2π(52.5)(3)
= 315 π m²
Conical part:
The radius of the conical part = 52.5 m
Slant height of the conical part = 53 m
Curved Surface-area of the conical part = πrl
= π (52.5) (53)
= (2782.5) π
Area of the canvas required :
Area of the canvas required = CSA of the cylindrical part + CSA of the conical part
= 315π + (2782.5)π
= (3097.5)π m²
Hence, area of the canvas required = (3097.5)π m²
Problem 2 :
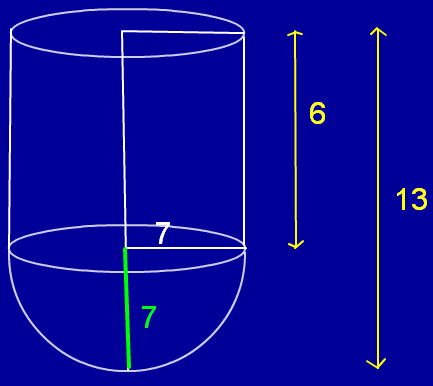
A vessel is in the form of hollow cylinder which has been surmounted on a hemispherical bowl.The diameter of a hemisphere is 14cm and the total height of a vessel is 13cm. Find the required curved surface area of the vessel.
Solution :
Diameter of the hemisphere = 14 cm
Radius of the hemisphere = 14/2 = 7 cm
Radius of the cylinder = radius of the hemisphere = 7 cm
Total height of the vessel = 14 cm
Total height of the vessel = height of the cylinder + radius of the hemisphere
13 = height of the cylinder + 7
Height of the cylinder = 13 - 7 = 6 cm
Curved Surface Area of the vessel = CSA of the cylinder + CSA of the hemisphere
= 2πrh + 2πr²
Here r = 7 and h = 6
= 2π(7)(6) + 2π (7)²
= 84π + 98π
= 182π
Hence, the Curved Surface Area of the Vessel = 182 π cm²
Problem 3 :
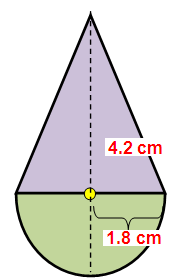
A play top is in the form of a hemisphere surmounted on a cone. The diameter of the hemisphere is 3.6 cm. The total height of the play top is 4.2 cm. Find its total surface area.
Solution :
Let r and h are radius and height of the cone.
diameter of the hemisphere = 3.6 cm
radius of hemisphere (r) = 3.6/2 = 1.8 cm
total height of the play top = 4.2cm
radius of hemisphere + height of cone = 4.2
1.8 + h = 4.2
h = 4.2-1.8
h = 2.4 cm
Now we are going to find slant height of cone
l2 = r2+h2
= (1.8)2+ (2.4)2
= 3.24 + 5.76
l2 = 9
L = √(3 ⋅ 3)
L = 3 cm
To find the total surface area of the play top, we have to find the sum of curved surface area of hemisphere and curved surface area of cone.
Total surface area of play top = C.S.A of hemisphere + C.S.A of cone
= 2Πr2+Πrl
= Πr(2r+l)
= Π ⋅ (1.8) [2(1.8) + 3]
= Π ⋅ (1.8) (3.6+3)
= Π (1.8) (6.6)
= 11.88 Π cm2
Total surface area of the play top = 11.88 Π cm².
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Problems Involving Rational Exponents and Radicals
Jun 17, 21 10:07 AM
Problems Involving Rational Exponents and Radicals
-
Factoring 4th Degree Polynomials
Jun 17, 21 08:11 AM
Factoring 4th Degree Polynomials - Concept - Examples with Step by Step Explanation
-
Finding Profit or Loss Percentage Worksheet
Jun 17, 21 05:47 AM
Finding Profit or Loss Percentage Worksheet
