PROBLEMS ON SPECIAL RIGHT TRIANGLES

Special right triangles are the triangles whose angle measures are

45° - 45° - 90° (or) 30° - 60° - 90°

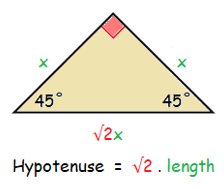
45° - 45° - 90° triangle theorem :

In a 45° - 45° - 90° triangle, the hypotenuse is √2 times as long as each length.

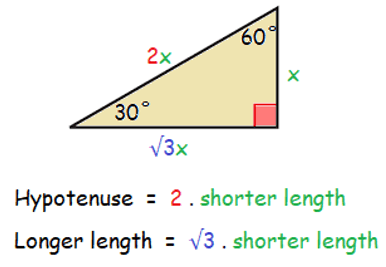
30˚- 60˚- 90˚ triangle theorem :

In a 30° - 60° - 90° triangle, the hypotenuse is twice as long as the shorter length, and the longer length is √3 times as long as the shorter length.

Example 1 :

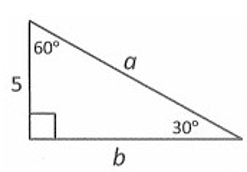
Solution :

Given triangle is a 30˚-60˚-90˚ triangle.

Finding the value of a :

By 30˚-60˚-90˚ triangle theorem,

hypotenuse = 2 . shorter length

Here hypotenuse = a, and shorter length = 5.

a = 2 . 5

a = 10

So, the value of a is 10.

Finding the value of b :

By 30˚-60˚-90˚ triangle theorem,

longer length = √3 . shorter length

Here longer length = b, and shorter length = 5.

b = √3 . 5

b = 5√3

So, the value of b is 5√3.

Example 2 :

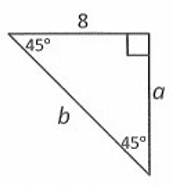
Solution :

Given triangle is a 45˚-45˚-90˚ triangle.

Finding the value of a :

Since the given triangle has base angles that are equal, the two sides' lengths are equal.

a = 8

Finding the value of b :

By 45˚-45˚-90˚ triangle theorem,

hypotenuse = √2 . length

Here hypotenuse = b, and length = 8

b = √2 . 8

b = 8√2

Example 3 :

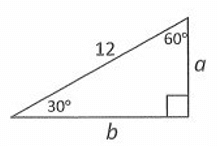
Solution :

Given triangle is a 30˚-60˚-90˚ triangle.

Finding the value of a :

By 30˚-60˚-90˚ triangle theorem,

hypotenuse = 2 . shorter length

Here hypotenuse = 12 and shorter length = a.

12 = 2 . a

a = 6

Finding the value of b :

By 30˚-60˚-90˚ triangle theorem,

longer length = √3 . shorter length

Here longer length = b and shorter length(a) = 6.

b = √3 . 6

b = 6√3

Example 4 :

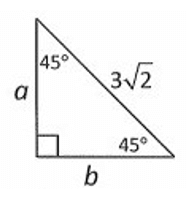
Solution :

Given triangle is a 45˚-45˚-90˚ triangle.

Finding the value of a :

By 45˚-45˚-90˚ triangle theorem,

hypotenuse = √2 . length

Here hypotenuse = 3√2 and length = a.

3√2 = √2 . a

3√2/√2 = a

a = 3

Finding the value of b :

Since the given triangle has base angles that are equal, the two sides' lengths are equal.

b = 3

Example 5 :

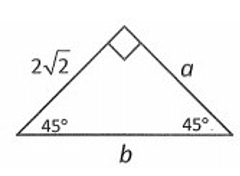
Solution :

Given triangle is a 45˚-45˚-90˚ triangle.

Finding the value of a :

Since the given triangle has base angles that are equal, the two sides' lengths are equal.

a = 2√2

Finding the value of b :

By 45˚-45˚-90˚ triangle theorem,

hypotenuse = √2 . length

Here hypotenuse = b and length = 2√2.

b = √2 . 2√2

b = 2 . 2

b = 4

Example 6 :

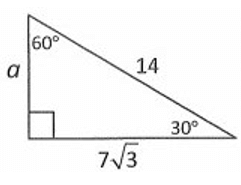
Solution :

Given triangle is a 30˚-60˚-90˚ triangle.

Finding the value of a :

By 30˚-60˚-90˚ triangle theorem,

hypotenuse = 2 . shorter length

Here hypotenuse = 14 and shorter length = a.

14 = 2 . a

a = 7

Example 7 :

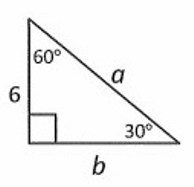
Solution :

Given triangle is a 30˚-60˚-90˚ triangle.

Finding the value of a :

By 30˚-60˚-90˚ triangle theorem,

Hypotenuse  =  2 . shorter length

Here hypotenuse = a, and shorter length = 6.

a = 2 . 6

a = 12

So, the value of a is 12.

Finding the value of b :

By 30˚-60˚-90˚ triangle theorem,

longer length = √3 . shorter length

Here longer length = b and shorter length = 6.

b = √3 . 6

b = 6√3

Example 8 :

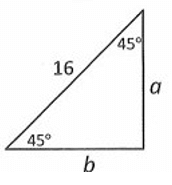
Solution :

Given triangle is a 45˚-45˚-90˚ triangle.

Finding the value of a :

By 45˚-45˚-90˚ triangle theorem,

hypotenuse = √2 . length

Here hypotenuse = 16 and length = a.

16 = √2 . a

a = 16/√2

To rationalize denominator in 16/√2, multiply numerator and denominator by √2.

a = (16/√2) . (√2/√2)

a = 16√2/2

a = 8√2

Finding the value of b :

Since the given triangle has base angles that are equal, the two sides' lengths are equal.

b = 8√2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.