PROBLEMS ON RIEMANN INTEGRAL

Consider a real-valued, bounded function f(x) defined on the closed and bounded interval[a, b], a < b.

The function f(x) need not have the same sign on [a,b] that is, f(x) may have positive as well as negative values on [a, b] .

Partition the interval [a, b] into n subintervals

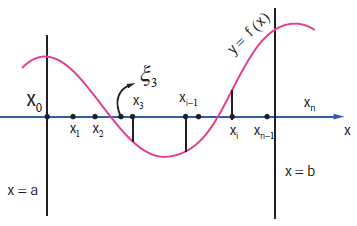
[x₀, x₁], [x₁, x₂].................,[x_n-2, x_n-1], [x_n-1, x_n] such that a = x₀ < x₁ < x₂ <.......x_n-1 < x_n = b

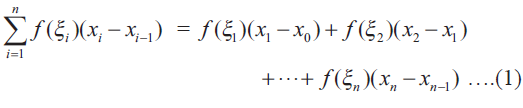
The sum in (1) is called a Riemann sum of f(x) corresponding to the partition

[x₀, x₁], [x₁, x₂].................,[x_n-2, x_n-1], [x_n-1, x_n] 

Left End Rule

By choosing Σ_i = x_i-1, i = 1, 2,...........n, we have

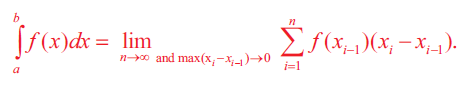
The above equation is known as the left-end rule for evaluating the Riemann integral.

Right End Rule

By choosing Σ_i = x_i-1, i = 1, 2,...........n, we have

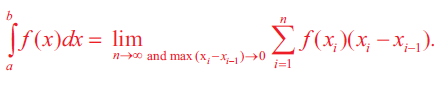
The above equation is known as the right-end rule for evaluating the Riemann integral.

Midpoint Rule

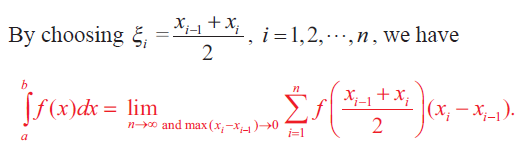
The above equation is known as the mid-point rule for evaluating the Riemann integral

Problem 1 :

Find an approximate value of integral 1 to 1.5 x dx by applying the left-end rule with the partition

{1.1, 1.2, 1.3, 1.4, 1.5}.

Solution : 

Here a = 1, b = 1.5, number of sub interval (n) = 5, f(x) = x

Width of interval (h) = Δx = 0.1

x₀ = 1, x₁ = 1.1, x₂ = 1.2, x₃ = 1.3, x₄ = 1.4

S = [f(x₀) + f(x₁) + f(x₂) + f(x₃) + f(x₄)]Δx

S = [f(1) + f(1.1) + f(1.2) + f(1.3) + f(1.4)](0.1)

= (1 + 1.1 + 1.2 + 1.3 + 1.4) (0.1)

= 6(0.1)

= 0.6

So, integral 1 to 1.5 x dx is approximately 0.6.

Problem 2 :

Find an approximate value of integral 1 to 1.5 x² dx by applying the right end rule with the partition 

{1.1, 1.2, 1.3, 1.4, 1.5}.

Solution :

Here a = 1, b = 1.5, number of sub interval (n) = 5

f(x) = x²

Width of interval (h) = Δx = 0.1

x₁ = 1.1, x₂ = 1.2, x₃ = 1.3, x₄ = 1.4, x₅ = 1.5

S = [f(x₁) + f(x₂) + f(x₃) + f(x₄) + f(x₅)]Δx

S = [f(1.1) + f(1.2) + f(1.3) + f(1.4) + f(1.5)](0.1)

= [(1.1)² + (1.2)² + (1.3)² + (1.4)² + (1.5)²](0.1)

= [1.21 + 1.44 + 1.69 + 1.96 + 2.25](0.1)

= 8.55(0.1)

=  0.855

Problem 3 :

Find an approximate value of integral 1 to 1.5 (2-x) dx by applying the mid point rule with the partition

{1.1, 1.2, 1.3, 1.4, 1.5}

Solution :

Here a = 1, b = 1.5, number of sub interval (n) = 5

f(x) = (2-x)

Width of interval (h) = Δx = 0.1

x₀ = 1, x₁ = 1.1, x₂ = 1.2, x₃ = 1.3, x₄ = 1.4, x₅ = 1.5

S = [f(x₀ + x₁)/2 + f(x₁ + x₂)/2 + f(x₂ + x₃)/2 + f(x₃ + x₄)/2 + f(x₄ + x₅)/2]Δx

S = [f(1+1.1)/2 + f(1.1+1.2)/2 + f(1.2+1.3)/2 + f(1.3+1.4)/2 + f(1.4+1.5)/2]Δx

S = [f(1.05) + f(1.15) + f(1.25) + f(1.35) + f(1.45)](0.1)

= [(2-1.05) + (2-1.15) + (2-1.25) + (2-1.35) + (2-1.45)](0.1)

= (0.95+0.85+0.75+0.65+0.55)(0.1)

= 3.75(0.1)

= 0.375

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.