PROBLEMS ON MATHEMATICAL INDUCTION

Question 1 :

Using the Mathematical induction, show that for any natural number n ≥ 2,

[1/(1 + 2)] + [1/(1 + 2 + 3)] + [1/(1 + 2 + 3 + 4)]  + · · · + [1/(1 + 2 + 3 + · · · + n)]  =  (n − 1)/(n + 1)

Solution :

Let p(n) =  [1/(1 + 2)] + [1/(1 + 2 + 3)] + [1/(1 + 2 + 3 + 4)]  + · · · + [1/(1 + 2 + 3 + · · · + n)]   =  (n − 1)/(n + 1)

Step 1 :

put n = 2

p(2)  =  p(n) =  [1/(1 + 2)]  =  (2 − 1)/(2 + 1)

  1/3  =  1/3

Hence p(2) is true.

Step 2 :

Let us assume that the statement is true for n = k

p(k) =  [1/(1 + 2)] + [1/(1 + 2 + 3)] + [1/(1 + 2 + 3 + 4)]  + · · · + [1/(1 + 2 + 3 + · · · + k)]   =  (k − 1)/(k + 1)  ----(1)  

We need to show that P(k + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = k + 1

p(k+1) 

p(n) =  [1/(1 + 2)] + [1/(1 + 2 + 3)] + [1/(1 + 2 + 3 + 4)]  + · · · + [1/(1 + 2 + 3 + · · · + (k+1))]   =  (n − 1)/(n + 1)

By applying (1) in this step, we get

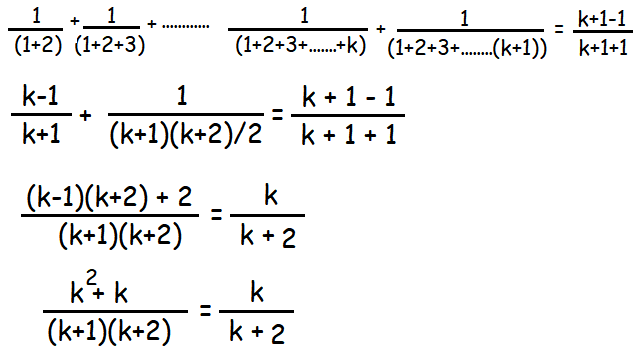
k(k+1)/(k+1)(k+2)  =  k/(k+2)

k/(k+2)  =  k/(k+2)

Hence, by the principle of mathematical induction  n ≥ 2,

[1/(1 + 2)] + [1/(1 + 2 + 3)] + [1/(1 + 2 + 3 + 4)]  + · · · + [1/(1 + 2 + 3 + · · · + n)]  =  (n − 1)/(n + 1)

Question 2 :

Using the Mathematical induction, show that for any natural number n,

[1/(1.2.3)]+[1/(2.3.4)]+[1/(3.4.5)]+ · · · +[1/(n.(n + 1).(n + 2))]

   =  n(n + 3)/4(n + 1)(n + 2)

Solution :

Let p(n)  = [1/(1.2.3)]+[1/(2.3.4)]+[1/(3.4.5)]+ · · · +[1/(n.(n + 1).(n + 2))]  =  n(n + 3)/4(n + 1)(n + 2)

Step 1 :

Put n = 1

[1/(1.(1 + 1).(1 + 2))]  =  1(1 + 3)/4(1 + 1)(1 + 2)

1/(1.2.3)  =  1(4)/4(2)(3)

1/(1.2.3) =  1/(1.2.3)

Hence p(1) is true.

Step 2 :

Let us assume that the statement is true for n = m

[1/(1.2.3)]+[1/(2.3.4)]+[1/(3.4.5)]+ · · · +[1/(m.(m+1).(m+2))]  =  m(m + 3)/4(m + 1)(m + 2)  --(1)  

We need to show that P(m + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = m + 1

p(m+1) 

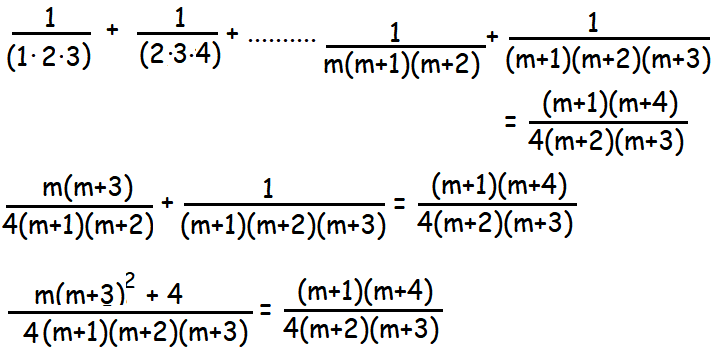
By expanding L.H.S, we get 

  =  (m(m²+6m+9) + 4)/4(m+1)(m+2)(m+3)  

  =  (m³ + 6m² + 9m + 4)/4(m+1)(m+2)(m+3)  

  =  (m+1)²(m+4)/4(m+1)(m+2)(m+3)  

  =  (m+1)(m+4)/4(m+1)(m+2)(m+3)  --->R.H.S

Hence, by the principle of mathematical induction [1/(1.2.3)]+[1/(2.3.4)]+[1/(3.4.5)]+ · · · +[1/(n.(n + 1).(n + 2))]

   =  n(n + 3)/4(n + 1)(n + 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.