PROBLEMS ON FUNCTIONS AND LINEAR EQUATIONS

Problem 1 :

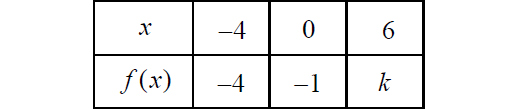
In the table above, find the value of k.

Solution :

Since f(x) is a linear function, its graph will be a straight line. The slope of a straight line at any point on it will be same. So, the slope between (-4, -4) and (0, -1) equals the slope between (0, -1) and (6, k).

Formula to find the slope of a line joining two points :

Slope between (-4, -4) and (0, -1) :

Substitute (x₁, y₁) = (-4, -4) and (x₂, y₂) = (0, -1) into the above formula.

Slope between (0, -1) and (6, k) :

Substitute (x₁, y₁) = (0, -1) and (x₂, y₂) = (6, k) into the above formula.

(1) = (2)

Problem 2 :

The graph of a line in the xy-plane has slope ⅓ and contains the point (9, 1). The graph of a second line passes through the points (-2, 4) and (5, -3). If the two lines intersect at (a, b), what is the value of a + b.

Solution :

Point-slope form equation of a line :

y - y₁ = m(x - x₁)

Substitute m = ⅓ and (x₁, y₁) = (9, 1) to get the equation of the first line.

y - 1 = ⅓(x - 9)

y - 1 = (⅓)x - (⅓)9

y - 1 = (⅓)x - 3

y = (⅓)x - 2 ----(1)

Substitute (x₁, y₁) = (-2, 4) and (x₂, y₂) = (5, -3) into slope formula to get the slope of the second line.

m = -1

Substitute m = -1 and (x₁, y₁) = (-2, 4) into point-slope form equation of a line to get the equation of the second line.

y - 4 = -1[x - (-2)]

y - 4 = -1(x + 2)

y - 4 = -x - 2

y = -x + 2 ----(2)

Solve (1) and (2).

(1) = (2)

y = y

(⅓)x - 2 = -x + 2

Multiply both sides by 3.

3[(⅓)x - 2] = 3(-x + 2)

3[(⅓)x] - 3(2) = -3x + 6

x - 6 = -3x + 6

4x = 12

x = 3

Substitute x = 3 into (2).

y = -3 + 2

y = -1

The point of intersection is (3, -1).

(a , b) = (3, -1)

a + b = 3 + (-1)

a + b = 3 - 1

a + b = 2

Problem 3 :

Which of the following expressions is equal to 0 for some value of x?

(A)  5 + |x + 5|

(B)  5 + |x - 5|

(C)  -5 + |x + 5|

(D)  -5 - |x - 5|

Solution :

We know that the absolute value of any non zero number (positive r negative) is always a positive number.

The expressions |x + 5| or |x - 5| can never be negative. Thus, 5 + |x + 5| or 5 + |x - 5| can not be equal to zero. The expression -|x - 5| can never be a positive number. Thus, -5 - |x - 5| can not be equal to zero.

So, -5 + |x + 5| must be zero.

-5 + |x + 5| = 0

|x + 5| = 5

x + 5 = 5  or  x + 5 = -5

x = 0  or  x = -10

Therefore, the correct answer is option (C).

Problem 4 :

Line k in the xy-plane contains points from each of the Quadrants I, III, and IV, but no points from Quadrant II. Which of the following must be true?

(A)  The slope of line k is zero.

(B)  The slope of line k is undefined.

(C)  The slope of line k is positive.

(D)  The slope of line k is negative.

Solution :

Draw a line in xy-plane such that it contains the points in Quadrants I, III, and IV, but no points from Quadrant II.

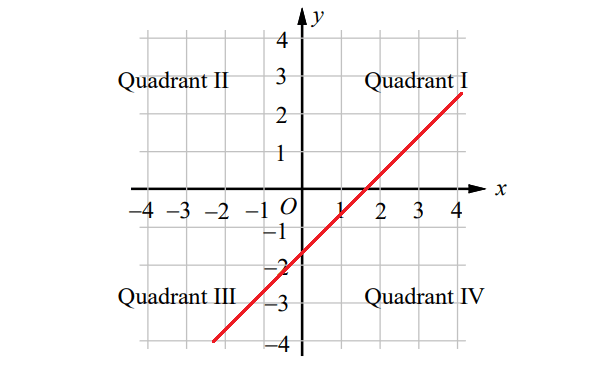
The line contains the points in Quadrants I, III, and IV, but no points from Quadrant II is a rising line and its slope is POSITIVE.

Therefore, the correct answer is option (C).

Problem 5 :

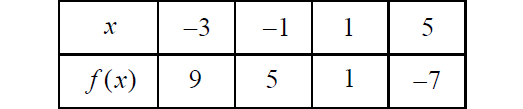
The table above shows some values of the linear function f. Which of the following defines f?

(A)  f(x) = 2x - 3

(B)  f(x) = -2x + 3

(C)  f(x) = 2x - 1

(D)  f(x) = -2x + 1

Solution :

Chosee any two points from the table above and find the slope.

Substitute (x₁, y₁) = (-3, 9) and (x₂, y₂) = (1, 1) into slope formula to get the slope of the second line.

m = -2

Use the slope m = -2 and choose one of the points from the table to find the equation of the line in point-slope form and convert it to slope-intercept form.

Substitute m = -2 and (x₁, y₁) = (1, 1) into point-slope form equation of a line.

y - y₁ = m(x - x₁)

y - 1 = -2(x - 1)

y - 1 = -2x + 2

y = -2x + 3

Replace y by f(x).

f(x) = -2x + 3

Therefore, the correct answer is option (B).

Problem 6 :

If f(x) = -6x + 1, find the expression which is equal to

Solution :

f(x) = -6x + 1

Replace x by ½x + 1.

Questions 7 and 8 refer to the following information.

The graph below shows the relationship between the height of paraglider H, in feet, and time m, in minutes.

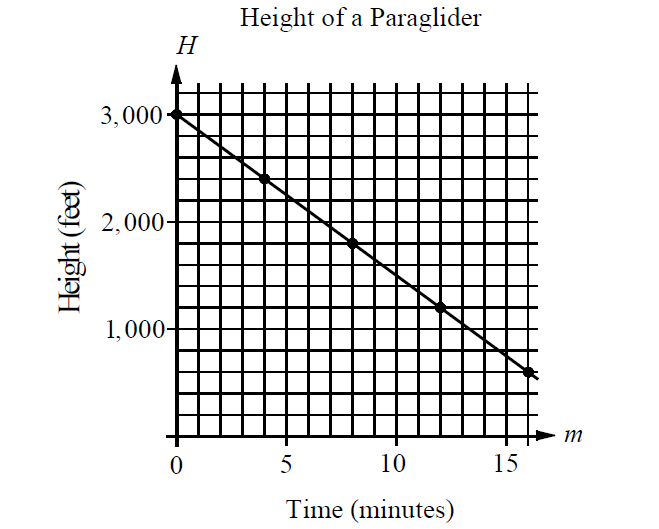
Problem 7 :

Which of the following represents the relationship between H and m?

(A)  H = -100m + 3000

(B)  H = -150m + 3000

(C)  H = -175m + 3000

(D)  H = -225m + 3000

Solution :

Chosee any two points on the line and find the slope.

Substitute (x₁, y₁) = (0, 3000) and (x₂, y₂) = (4, 2400) into slope formula to get the slope of the second line.

m = -150

Use the slope m = -2 and choose one of the points from the table to find the equation of the line in point-slope form and convert it to slope-intercept form.

Substitute m = -150 and (x₁, y₁) = (0, 3000) into point-slope form equation of a line.

y - y₁ = m(x - x₁)

y - 3000 = -150(x - 0)

y - 3000 = -150x

y = -150x + 3000

In the graph shown above, instead of x and y we have m and H respectively. Replace y by H and x by m.

H = -150m + 3000

Therefore, the correct answer is option (B).

Problem 8 :

If the height of the paraglider is 1,350 feet, which of the following best approximates the time the paraglider has been flying?

(A)  10 minutes

(B)  10 minutes and 30 seconds

(C)  11 minutes

(D)  11 minutes and 30 seconds

Solution :

From the above problem, the equation of the line is

H = -150m + 3000

Substitute H = 1350.

1350 = -150m + 3000

150m = 1650

m = 11 minutes

Therefore, the correct answer is option (C).

Problem 9 :

A line in the xy-plane passes through the point (1, -2) and has a slope of ⅓. Which of the following points lies on the line? 

(A)  (3, -2)

(B)  (2, -⁴⁄₃)

(C)  (0, -2)

(D)  (-1, -⁸⁄₃)

Solution :

Point-slope form equation of a line :

y - y₁ = m(x - x₁)

Substitute m = ⅓ and (x₁, y₁) = (1, -2) into point-slope form equation of a line.

y - (-2) = (⅓)(x - 1)

y + 2 = (⅓)x - ⅓

y = (⅓)x - ⅓ - 2

y = (⅓)x - ⁷⁄₃

Check the point in each option with the above equation.

(A)  (3, -2) :

-2 = (⅓)(3) - ⁷⁄₃

-2 = 1 - ⁷⁄₃

-2 = -⁴⁄₃

(false)

(B)  (2, -⁴⁄₃) :

-⁴⁄₃ = (⅓)(2) - ⁷⁄₃

-⁴⁄₃ = ⅔ - ⁷⁄₃

-⁴⁄₃ = -⁵⁄₃

(false)

(C)  (0, -2) :

-2 = (⅓)(0) - ⁷⁄₃

-2 = 0 - ⁷⁄₃

-2 = -⁷⁄₃

(false)

(D)  (-1, -⁸⁄₃) :

-⁸⁄₃ = (⅓)(-1) - ⁷⁄₃

-⁸⁄₃ = -⅓ - ⁷⁄₃

-⁸⁄₃ = -⁸⁄₃

(true)

Therefore, the correct answer is option (D).

Problem 10 :

f(x) = ax + 2

In the function above, a is a constant. If f(-1) = 4, find the value of f(-½).

Solution :

f(x) = ax + 2

f(-1) = a(-1) + 2

f(-1) = -a + 2

Given : f(-1) = 4.

4 = -a + 2

a = -2

Then the given function is

f(x) -2x + 2

Substitute x = -½.

f(-½) = -2(-½) + 2

f(-½) = 1 + 2

f(-½) = 3

Problem 11 :

If the slope of the line in the -xyplane that passes through the points (2, -4) and (6, k) is ³⁄₂, what is the value of k?

Solution :

m = ³⁄₂

Use the slope formula.

Substitute (x₁, y₁) = (2, -4) and (x₂, y₂) = (6, k).

k + 4 = 6

k = 2

Problem 12 :

If (x, y) is the solution to the system of equations above, what is the value of x + y?

Solution :

Multiply the first equation by 3 and the second by 2.

Add the above two equations to get rid of x.

Least common multiple of (4, 3) = 12. Multiply both sides by 12 to get rid of the denominators 4 and 3.

-27y - 4y = -372

-31y = -372

y = 12

Substitute y = 12 into the second equation.

x = -6

(x, y) = (-6, 12)

x + y = -6 + 12

x + y = 6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.