PROBLEMS ON CYLINDER

A geometrical shape with two parallel straight sides having two circular parts such that one is at the top and the other is at the bottom.

Right Circular Cylindrical Solid :

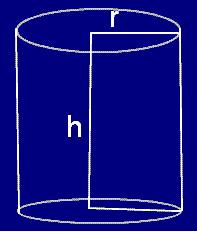
This one is a  solid which is being generated by rotating of rectangle about one of its sides. Consider the rectangle PQRS which is rotated about its side PQ and makes one complete rotation to reach the initial position. This rotation creates a right circular cylindrical solid.

Each and every of this right circular cylindrical solid is having two plane endings. The end of each plane is in a  circular shape and the endings of the planes are parallel.

End of each plane is known as the base of the above right circular cylindrical solid. A straight line that joins the centers of those two planes is called the axis.

The radius of the base circle is called as the radius of the right circular cylindrical solid.

The curved surface which joins the two planes ending is the lateral surface area or curved surface area.

In the above picture, the letters, r represents radius and h represents height.

Hollow Cylindrical Solid :

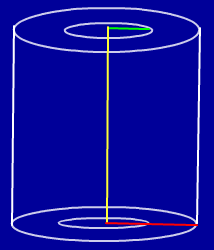
A solid which is being formed  by two co-axial piston chambers with the same height and same radii is called as hollow-cylindrical solid.  

Here "R" says the external radius and "r" says the internal radius of the cylinder.

In the above picture of a hollow-cylindrical shape, the green colored line represents an internal radius, the red colored  line represents an external radius and the yellow line represents the height of the hollow cylindrical solid.

Role of radius and height in finding areas and volumes :

When we want to find areas and volumes , these two values "r" and "h" that radius and height plays a vital role. When we know the radius and height, we can use the formula and find the areas and volumes.   

Problem 1 :

A solid right circular cylinder has radius of 14 cm and height of 8 cm. Find its curved surface area and total surface area.

Solution :

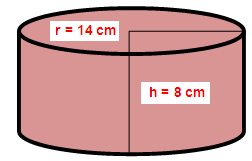
Radius  (r) = 14 cm

Height (h) = 8 cm

Curved surface area   =  2 Π r h

=  2 ⋅ (22/7) ⋅ 14 ⋅ 8

=  2 ⋅ 22 ⋅ 2 ⋅ 8

=  704 sq.cm

Total surface area of cylinder  =  2 Π r (h + r)

=  2 ⋅ (22/7) ⋅ 14 ⋅ (8 + 14)

=  2 ⋅ (22/7) ⋅ 14 ⋅ 22

=  2 ⋅ 22 ⋅ 2 ⋅ 22

=  1936 sq.cm

Curved surface area  =  704 sq.cm

Total surface area  = 1936 sq.cm

Problem 2 :

The total surface area of solid cylinder is 616 cm² . And radius is 7cm, find the height.

Solution :

Total surface area of cylinder =  2 Π r (h + r)

Radius = 7 cm

Total surface area of solid cylinder = 616 cm²

2 x 22/7 x 7 (h + 7) = 616

44(h + 7) = 616

h + 7 = 616/44

h + 7 = 14

h = 14 - 7

h = 7 cm

So, the height of the cylinder is 7 cm.

Problem 3 :

Find the volume of a hollow cylinder having diameter 10 cm and 8 cm and height 7 cm

Solution :

Diameter of large cylinder = 10 cm

Radius of outer cylinder (R) = 5 cm

Diameter of small cylinder = 8 cm

Radius of inner cylinder (r) = 4 cm

height = 7 cm

Volume of hollow cylinder = Π h (R² - r²)

= (22/7) x 7 x  (5² - 4²)

= 22 x (25 - 16)

= 22 x 9

= 198 cm³

Problem 4 :

If the diameter and height of a cylinder is 8 m and 4 m, then find capacity of it in litres.

Solution :

To find the capacity, we have to find the volume of the cylinder.

Diameter = 8 m, radius = 4 m

height = 4 m

Volume of hollow cylinder = Π r² h

= (22/7) x 4² x 4

= 200.96 m³

1 m³ = 1000 liter

= 200.96 (1000)

= 200960 liters.

Problem 5 :

If the volume of a cylinder is 6237 cm³, and height 4.5 cm, find the radius of it

Solution :

Volume of cylinder = 6237 cm³

height = 4.5 cm

Π r² h = 6237

3.14 x r² (4.5) = 6237

r² = 6237 / (3.14 x 4.5)

r² = 441.4

r = 21 cm

So, the radius of the cylinder is 21 cm.

Problem 6 :

If the radius of a cylinder is doubled and height is halved then find its new volume.

Solution :

Radius and height of the cylinder will be r and h respectively.

Double the radius = 2r

Height is halved = h/2

Volume of cylinder = Π r² h

Volume of new cylinder = Π (2r)² (h/2)

= Π (4r²) (h/2)

= 2 Π r²h

When these changes happened, the old volume will become doubled.

Problem 7 :

If the ratio of base radius two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. Find the ratio of their volumes

Solution :

Let r₁ and r₂ be the radii of two cylinders.

Let h₁ and h₂ be the height of two cylinders.

Π r₁² h₁ : Π r₂² h₂

= Π (2r₂/3)² (5h₂/3) / Π r₂² h₂

= (4/9) (5/3)

= 20 / 27

= 20 : 27

So, the ratio between these two cylinders is 20 : 27.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.