PROBLEMS ON COMPOSITION OF FUNCTIONS

Problem 1 :

If f(x) = 2x - 1, g(x) = (x + 1)/2, show that

f o g = g o f = x

Solution :

From (1) and (2), 

f o g = g o f = x

Problem 2 :

If f(x) = x² - 1, g(x) = x - 2 find a, if g o f(a) = 1.

Solution :

g o f(a) = 1

g[f(a)] = 1

g[a² - 1] = 1

a² - 1 - 2 = 1

a² - 3 = 1

a² = 4

Take square root on both sides. 

a = ±2

Problem 3 : 

Find k, if f(k) = 2k - 1 and f o f(k) = 5.

Solution :

f o f(k) = 5

f[f(k)] = 5

f[2k - 1] = 5

2(2k - 1) - 1 = 5

4k - 2 - 1 = 5

4k - 3 = 5

4k = 8

k = 2

Problem 4 :

The suggested retail price of a new hybrid car is dollars. The dealership advertises a factory rebate of $2000 and a 10% discount.

(a)Write a function in terms of giving the cost of the hybrid car after receiving the rebate from the factory.

(b)Write a function in terms of giving the cost of the hybrid car after receiving the dealership discount.

Solution :

a) Let p be the price of hybrid car in dollars.

Cost of hybrid car after receiving the rebate from the factory

= p - 2000

b) Price of the car after receiving the dealership discount 

Since it 10 % discount, we pay 90% of the price.

The required price = 0.9p

Problem 5 :

A spherical weather balloon is being inflated in such a way that the radius is 

r = f(t) = 0.25 t + 3

where t is in seconds and r is in feet. The volume V of the balloon is the function

V(r) = (4/3)π r³

a) What is the radius when the inflation process begins ?

b) Write the equation to describe the composition V∘f that gives the volume at t seconds after the inflation begins.

c) What is the volume of the balloon 10 seconds after inflation begins ?

d)  In how many seconds will the volume be 400 cubic feet ? 

Solution :

r = f(t) = 0.25 t + 3

V(r) = (4/3)π r³

a) when inflation begins, t = 0

f(0) = 0.25(0) + 3

r = f(0) = 3

When inflation begins, the radius is 3 feet.

b)  V∘f = V(f)

= V(0.25 t + 3)

Applying r as 0.25t + 3 in the function V(r)

=  (4/3)π ((0.25 t + 3)³

c) Volume of balloon after 10 seconds

V(10) = (4/3)π (10)³

= 3140 cubic feet

d) When volume = 400 cubic feet

400 = (4/3)π r³

r³ = 400 (3/4) (1/π)

r³ = 100 (3) (1/3.14)

r³ = 95.54

r = 4.57 feet

Problem 6 :

A circle is shrinking size in such a way that the radius r (in feet) is a function of time t (in minutes), given by the equation 

r = f(t) = 1/(t + 1)

The area of the circle is given by

A(r) = π r²

so the area is also a function of time, given by (A ∘ f)(t)

a) Write the formula for (A ∘ f)(t)

b) What is the area at the end of one minute ? Two minutes ?

c) For what value of t is the area π/25 ?

Solution :

Given that,

r = f(t) = 1/(t + 1)

A(r) = π r²

(A ∘ f)(t) = A[f(t)]

= A [1/(t + 1)]

= π [1/(t + 1)]²

(A ∘ f)(t) = π/(t + 1)²

b) Area at the end of one minute, then apply t = 1 in the composition function.

(A ∘ f)(1) = π/(1 + 1)²

= π/2²

= π/4

c)  (A ∘ f)(t) = π/(t + 1)²

π/25 = π/(t + 1)²

(t + 1)² = 25

t + 1 = 5

t = 5 - 1 

t = 4

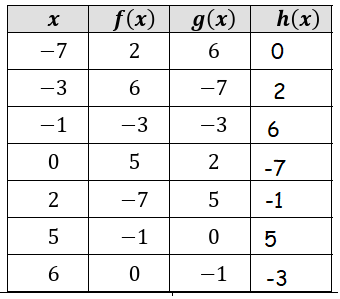
Problem 7 :

Fill in the following table, given that ℎ(𝑥) = 𝑓(𝑔(x)) .

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.