PROBLEMS ON COMPLEMENTARY AND SUPPLEMENTARY ANGLES

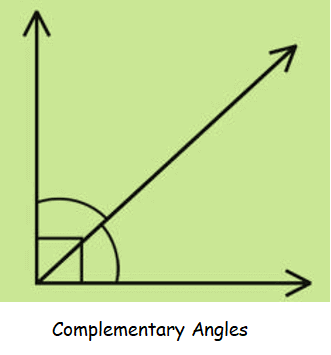
Complementary Angles :

The two angles whose sum is 90˚

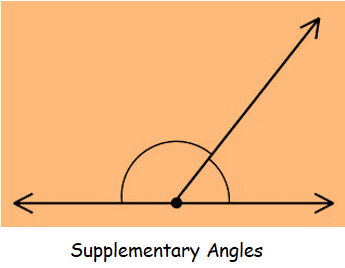
Supplementary Angles :

The two angles whose sum is 180˚

In each case. find the missing angle :

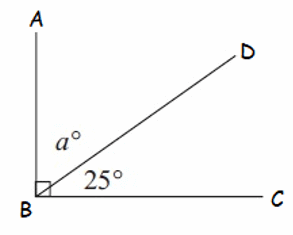
Example 1 :

Solution :

In the diagram shown above, ∠ABD and∠DBC are complementary angles.

∠ABD + ∠DBC = 90°

Substitute ∠ABD = a° and ∠DBC = 25°.

a° + 25° = 90°

Subtract 25° from both sides.

a° = 65°

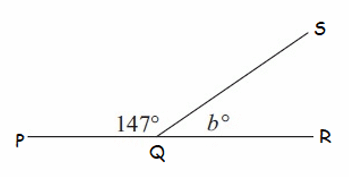
Example 2  :

Solution :

In the diagram shown above, ∠PQS and∠SQR are complementary angles.

∠PQS + ∠SQR = 180°

Substitute ∠PQS = 147° and ∠SQR = b°.

147° + b° = 180°

Subtract 147° from both sides.

b° = 33°

Example 3 :

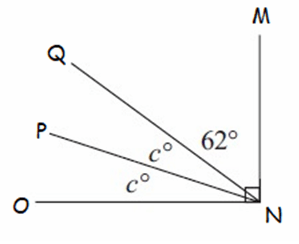
Solution :

In the diagram shown above, ∠MNQ, ∠QNP, and ∠PNO are complementary angles.

∠MNQ + ∠QNP + ∠PNO = 90°

Substitute ∠MNQ = 62°, ∠QNP = c° and ∠PNO = c°.

62° + c° + c° = 90°

62° + 2c° = 90°

Subtract 62° from both sides.

2c° = 28°

Divide both sides by 2.

c = 14°

Example 4 :

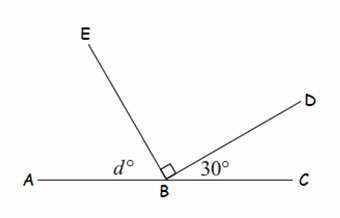
Solution :

In the diagram shown above, ∠ABE, ∠EBD and ∠DBC are supplementary angles.

∠ABE + ∠EBD + ∠DBC = 180°

Substitute ∠ABE = d°, ∠EBD = 90° and ∠DBC = 30°.

d° + 90° + 30° = 180°

d° + 120° = 180°

Subtract 120° from both sides.

d° = 60°

Example 5 :

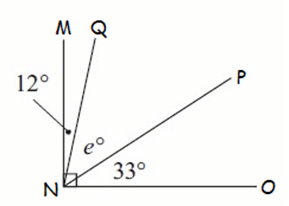
Solution :

In the diagram shown above, ∠MNQ, ∠QNP, and ∠PNO are complementary angles.

m∠MNQ + m∠QNP + m∠PNO = 90°

Substitute ∠MNQ = 12°, ∠QNP = e° and ∠PNO = 33°.

12° + e° + 33° = 90°

45° + e° = 90°

Subtract 45° from both sides.

e = 45°

Example 6 :

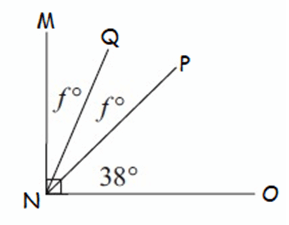
Solution :

In the diagram shown above, ∠MNQ, ∠QNP, and ∠PNO are complementary angles.

∠MNQ + ∠QNP + ∠PNO = 90°

Substitute ∠MNQ = f°, ∠QNP = f° and ∠PNO = 38°.

f° + f° + 38° = 90°

2f° + 38° = 90°

Subtract 38° from both sides.

2f° = 52°

Divide both sides by 2.

f = 26°

Example 7 :

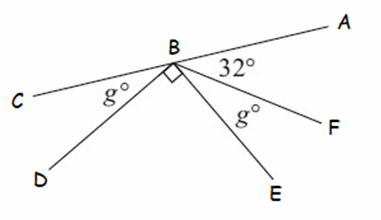
Solution :

In the diagram shown above, ∠ABF, ∠FBE, ∠EBD and ∠DBC are supplementary angles.

∠ABF + ∠FBE + ∠EBD + ∠DBC = 180°

Substitute ∠ABF = 32°, ∠EBD = 90° and∠FBE = ∠DBC = g°.

32° + g° + 90° + g° = 180°

2g° + 122° = 180°

Subtract 122° from both sides.

2g˚ = 58°

Divide both sides by 2.

g° = 29°

Example 8 :

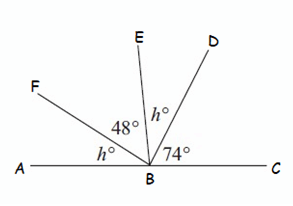
Solution :

∠ABF, ∠FBE, ∠EBD and ∠DBC are supplementary angles.

∠ABF + ∠FBE + ∠EBD + ∠DBC = 180°

Substitute ∠ABF = h°, ∠FBE = 48°, ∠EBD = h°, ∠DBC = 74°

h° + 48° + h° + 74° = 180°

2h° + 122° = 180°

Subtract 122° from both sides.

2h° = 58°

Divide both sides by 2.

h = 29°

Example 9 :

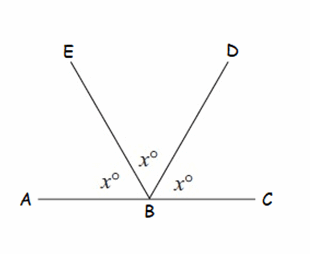
Solution :

In the diagram shown above, ∠ABE, ∠EBD and ∠DBC are supplementary angles.

∠ABE + ∠EBD + ∠DBC = 180°

Substitute ∠ABE = ∠EBD = ∠DBC = x°.

x° + x° + x° = 180°

3x° = 180˚

Divide both sides by 3.

x = 60°

Example 10 :

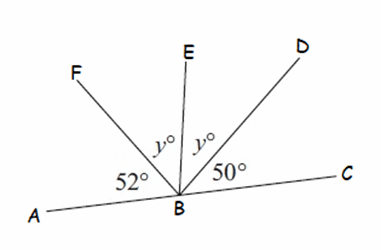
Solution :

In the diagram shown above, ∠ABF, ∠FBE, ∠EBD and ∠DBC are supplementary angles.

∠ABF + ∠FBE + ∠EBD + ∠DBC = 180°

Substitute ∠ABF = 52°, ∠FBE = ∠EBD = y°, ∠DBC = 50°.

52° + y° + y° + 50° = 180°

2y° + 102° = 180°

Subtract 102° from both sides.

2y° = 78°

Divide both sides by 2.

y = 39°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.