PROBLEMS ON CIRCLE THEOREMS

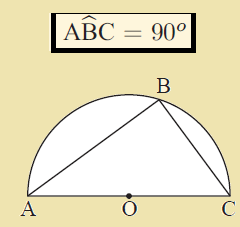
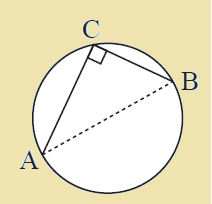
Angle in a semi-circle :

The angle in a semi-circle is a right angle.

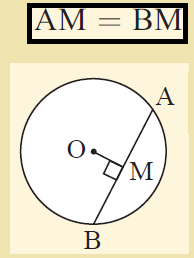
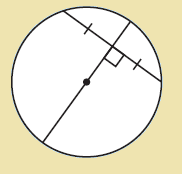
Chords of a circle :

The perpendicular from the centre of a circle to a chord bisects the chord.

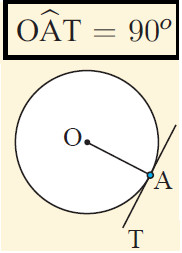
Radius tangent :

The tangent to a circle is perpendicular to the radius at the point of contact.

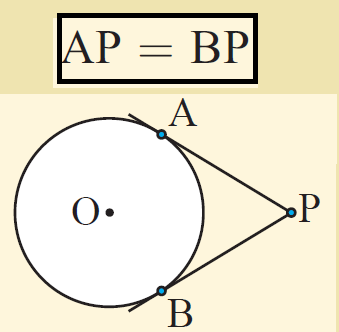
Tangents from an external point :

Tangents from an external point are equal in length.

If line segment [AB] subtends a right angle at C then the circle through A, B and C has diameter [AB].

The perpendicular bisector of a chord of a circle passes through its center

Find x in the given figures :

Example 1 :

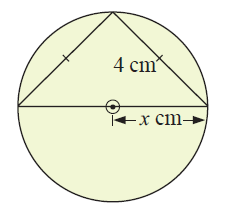
Solution :

Inside the circle, we have a isosceles triangle. Angle in a semicircle is a right angle.

Radius  =  x cm

(2x)²  =  4²+4²

4x²  =  16+16

4x²  =  32

x²  =  8

x  =  2√2

Example 2 :

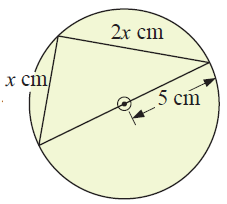
Solution :

Angle in a semicircle is a right angle.

Using Pythagorean theorem :

Radius of the circle  =  5 cm, diameter  =  10 cm.

x² + (2x)²  =  10²

x² + 4x²  =  100

5x²  =  100

x²  =  20

x  =  2√5

Example 3 :

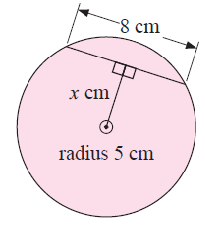
Solution :

Perpendicular drawn from the center of the circle to the chord divides the chord into two equal half.

Radius of the circle  =  5 cm, length of perpendicular  =  x

Half of length of chord  =  4 cm

4² + x²  =  5²

16 + x²  =  25

x²  =  25-16

x²  =  9

x  =  3

Example 4 :

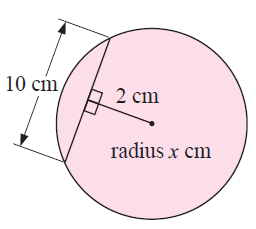
Solution :

Perpendicular drawn from the center of the circle to the chord divides the chord into two equal half.

Radius of the circle  =  x cm, length of perpendicular  =  2

Half of length of chord  =  5 cm

5² + 2²  =  x²

25 + 4  = x²

x²  =  29

x  =  √29

Example 5 :

Find a and b

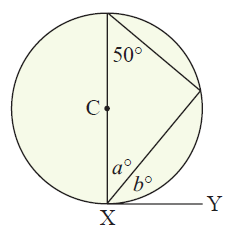
Solution :

In a triangle,

50 + 90 + a  =  180

a+140  =  180

a  =  180-140

a  =  40

a+b  =  90

40+b  =  90

b  =  50

Example 6 :

Find a and b

Solution :

Angle in a semicircle is 90 degree.

a+30  =  90

a  =  60

In the large triangle,

40+90+unknown angle  =  180

unknow angle  =  180-130

unknow angle  =  50

unknown + b  =  90

b  =  90-50

b  =  40

Example 7 :

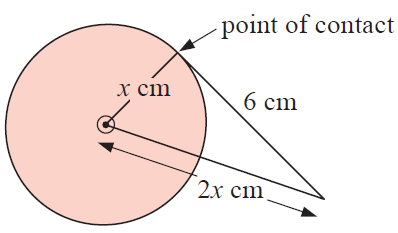
Solution :

The tangent to a circle is perpendicular to the radius at the point of contact.

x² + 6²  =  (2x)²

x² + 36  =  4x²

36  =  3x²

x²  =  12

x  =  2√3

Example 8 :

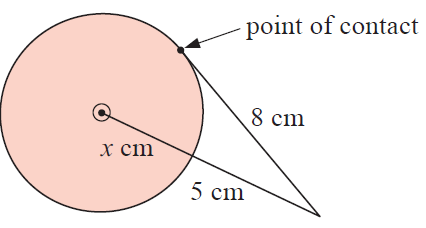
Solution :

x²+8²  =  (x+5)²

x²+64  =  x²+10x+25

64-25  =  10x

10x  =  39

x  =  39/10

x  =  3.9 cm

Example 9 :

Two circles have a common tangent with points of contact at A and B. The radii are 4 cm and 2 cm respectively. Find the distance between the centers, given that AB is 7 cm.

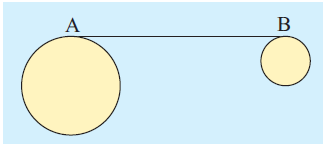
Solution :

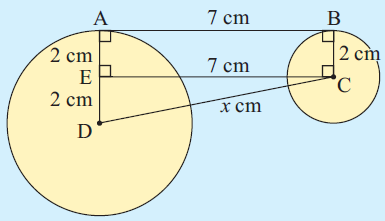
For centers C and D, we draw BC , AD, CD and CE || AB. ABCD is a rectangle.

CE = 7 cm

AD = 4 cm

AD = AE + ED

4 = 2 + ED

ED = 4 - 2

ED = 2 cm

In triangle DEC,

DC² = DE² + EC²

x² = 2² + 7²

= 4 + 49

x² = 53

x = √53

x = 7.3

The distance between the centers is 7.3 cm.

Example 10 :

In the given figure, AB = 1 cm and AC = 3 cm. Find the radius of the circle.

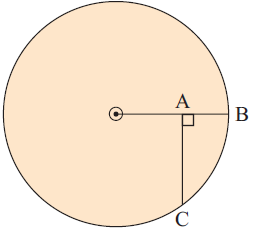
Solution :

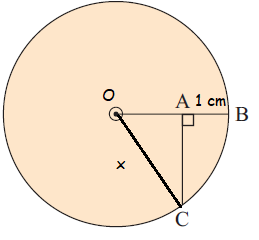
OB = OC = radii = x cm

OA = x - 1, AC = 3 cm

OC² = OA² + AC²

x² = (x - 1)² + 3²

x² = x² - 2x + 1 + 9

0 = -2x + 10

2x = 10

x = 10/2

x = 5 cm

So, the radius of the circle is 5 cm.

Example 11 :

The chord of the circle is 14 cm in length and 8 cm from the center of the circle. Find the radius of the circle.

Solution :

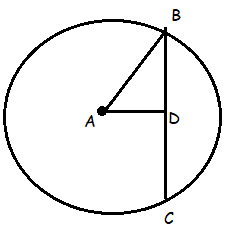
AD = 8 cm

BC = 14 cm, BD = 14/2 ==> 7 cm

In triangle ABD,

AB² = BD² + AD²

AB² = 7² + 8²

= 49 + 64

= 113

AB = √113

= 10.63 cm

Example 12 :

A circle has a chord of length 10 cm. The shortest distance from the circle's center to the chord is 5 cm. Find the radius of the circle.

Solution :

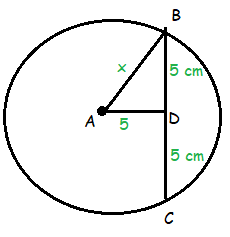
AD = 5 cm

BC = 10 cm, BD = 10/2 ==> 5 cm

In triangle ABD,

AB² = BD² + AD²

x² = 5² + 5²

= 25 + 25

= 50

x = √50

x = 5√2 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.