PROBLEMS ON CHAIN RULE IN PARTIAL DIFFERENTIATION

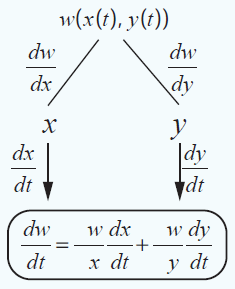
Suppose that W(x, y) is a function of two variables x, y having partial derivatives ∂W/∂x, ∂W/∂y. If both variables x, y are differentiable functions of a single variable t, then W is differentiable function t and 

Problem 1 :

If

w(x, y) = 6x³-3xy+2y², x = e^s, y = cos s, s ∈ ℝ

find dw/ds, and evaluate at s = 0.

Solution :

dw/ds = (∂w/∂x) (dx/ds) + (∂w/∂y) (dy/ds)

Applying the values in the formula, we get

= (18x²-3y)(e^s) + (-3x+4y)(-sin s)

= (18e^2s-3cos s)(e^s) + (-3e^s+4cos s)(-sin s)

= 18e^3s-3e^scos s +3e^ssin s - 4cos s sin s

At s = 0

= 18e³⁽⁰⁾-3e⁽⁰⁾cos 0 +3e⁽⁰⁾sin 0 - 4cos 0 sin 0

= 18-3

= 15

Problem 2 :

If

z(x,y) = x tan^-1(xy), x = t², y = se^t, s,t ∈ ℝ.

Find ∂z/∂s and ∂z/∂t at s = t = 1

Solution :

z(x, y) = x tan^-1(xy)

∂z/∂s = (∂z/∂x)(∂x/∂s) + (∂z/∂y)(∂y/∂s) ---(1)

∂z/∂x = x[1/(1+(xy)²)] y+ tan^-1(xy)(1)

∂z/∂x = [xy/(1+(xy)²)] + tan^-1(xy)

∂x/∂s = 0

∂z/∂y = x[1/(1+(xy)²)] x+ tan^-1(xy)(1)

∂z/∂y = [x²/(1+(xy)²)] + tan^-1(xy) (0)

∂z/∂y =  [x²/(1+(xy)²)]

 y = se^t

∂y/∂s = e^t

By applying the values in the formula, we get

=[x²/(1+(xy)²)] + tan^-1(xy)(0) + [x²/(1+(xy)²)] e^t

= [t⁴/(1+(t²se^t)²)] e^t

Applying the values of s and t, we get

= e/(1+e²)

∂z/∂s = (∂z/∂x)(∂x/∂s) + (∂z/∂y)(∂y/∂s) ---(2)

∂z/∂x = x[1/(1+(xy)²)] y+ tan^-1(xy)(1)

∂z/∂x = [xy/(1+(xy)²)] + tan^-1(xy)

∂x/∂t = 2t

∂z/∂y = x[1/(1+(xy)²)] x+ tan^-1(xy)(1)

∂z/∂y = [x²/(1+(xy)²)] + tan^-1(xy) (0)

∂z/∂y =  [x²/(1+(xy)²)]

∂y/∂t = se^t

∂z/∂t = {[xy/(1+(xy)²)] + tan^-1(xy)}2t + [x²/(1+(xy)²)]se^t

∂z/∂t = 2t{[t²(se^t)/(1+(t²(se^t))²)] + tan^-1(t²se^t)}2t + [t⁴/(1+(e^tse^t)²)]se^t

When s = t = 1

∂z/∂t = 2e/(1+e²) + 2tan^-1(e) + e/(1+e²)

∂z/∂t = 3e/(1+e²) + 2tan^-1(e)

Problem 3 :

Let

U(x, y) = e^x sin y

where x = st², y = s²t s,t ∈ ℝ. Find ∂U/∂s, ∂U/∂t and evaluate them at s = t = 1.

Solution :

∂U/∂s = (∂U/∂x)(∂x/∂s) + (∂U/∂y)(∂y/∂s) ----(1)

Applying the values in the formula above.

= (e^x sin y)t² + e^x cos y(2st)

= e^x[(t²sin y) + 2st cos y]

= te^x[t sin y + 2s cos y]

Applying the values of x and y, we get

= te^{st^2}[t sin (s²t) + 2s cos (s²t)]

Applying the value of s and t, we get

= te^{st^2}[sin (1) + 2cos (1)]

∂U/∂t = (∂U/∂x)(∂x/∂t) + (∂U/∂y)(∂y/∂t) ----(2)

x = st², y = s²t

∂x/∂t = 2st, ∂y/∂t = s²

Applying the values in the formula above.

= (e^x sin y)(2st) + e^x cos y(s²)

= e^x [2st sin y + cos y(s²)]

= e^{st^2} [2st sin (s²t) + cos (s²t)(s²)]

By applying the values of s and t, we get

= e [2sin (1) + cos (1)]

Problem 4 :

Let

z(x, y) = x³-3x²y³

where x = se^t, y = se^-t, s, t  ∈ ℝ. Find ∂z/∂s, ∂z/∂t.

Solution :

∂z/∂s = (∂z/∂x) (∂x/∂s) + (∂z/∂y) (∂y/∂s) ---(1)

= (3x²-6xy³)e^t -9x²y²e^-t

= 3e^tx²-6xy³e^t -9x²y²e^-t

Applying the values of x and y

= 3e^t(se^t)²-6(se^t)(se^-t)³e^t -9(se^t)²(se^-t)²e^-t

= 3s²e^3t-6s⁴e^-t -9s⁴e^-t

= 3s²e^t[e^2t-2s²e^-2t -3s²]

∂z/∂t = (∂z/∂x) (∂x/∂t) + (∂z/∂y) (∂y/∂t) ---(1)

∂x/∂t = se^t and ∂y/∂t = -se^-t

= (3x²-6xy³)se^t -9x²y²(-se^-t)

Applying the values of x and y

= (3s²e^2t-6s²)(se^t) - 9(s⁴)(-se^-t)

= 3s³e^3t-6s⁴e^-2t + 9s⁵e^-t

= 3s³[e^3t-2se^-2t +9s²e^-t]

Problem 5 :

W(x, y, z) = xy + yz + zx, x = u − v, y = uv, z = u + v, u,v  ∈ ℝ. Find ∂W/∂u, ∂W/∂v and evaluate them at (1/2, 1).

Solution :

∂W/∂u = (∂W/∂x) (∂x/∂u) + (∂W/∂y) (∂y/∂u) + (∂W/∂z) (∂z/∂u)

∂W/∂u = (y+z)(1) + (x+z)(v) + (y+x)(1)

∂W/∂u = 2y+x+z + (x+z)(v)

Applying the values of x = u − v, y = uv, z = u + v

∂W/∂u = 2uv+u-v+u+v + (u-v+u+v)(v)

∂W/∂u = 2uv+2u+uv-v²+uv+v²

∂W/∂u = 4uv+2u

∂W/∂u at (1/2, 1) = 4(1/2)(1)+2(1/2)

= 2 + 1

= 3

∂W/∂v = (∂W/∂x) (∂x/∂v) + (∂W/∂y) (∂y/∂v) + (∂W/∂z) (∂z/∂v)

∂W/∂u = (y+z)(-1) + (x+z)(u) + (y+x)(1)

Simplifying and applying the values of 

x = u − v, y = uv, z = u + v

∂W/∂u = -y-z + (u-v+u+v)(u) + (uv+u-v)(1)

∂W/∂u = -uv-u-v + 2u²+ uv+u-v

∂W/∂u = -2v + 2u²

∂W/∂u at (1/2, 1) = -2(1) + 2(1/2)²

= -2 + 1/2

=  -3/2

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.