PROBLEMS INVOLVING ANGLE OF ELEVATION AND DEPRESSION

Problem 1 :

From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. (√3 = 1.732)

Solution :

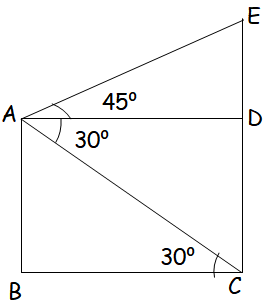
AB = 13 m  =  DC

In triangle AED,

tan 45  =  ED/AD

1  =  ED/AD

AD =  ED  --(1)

In triangle ABC,

tan 30  =  AB/BC

1/√3  =  13/BC

BC  =  13√3  ----(2)

AD  =  BC

By applying the value of AD in (1), we get 

ED  =  13√3 

height of second tree  =  ED + DC

  =  13√3 + 13

  =  13(√3 + 1)

  =  13(1.732 + 1)

  =  13(2.732)

  =  35.516 m

Hence the height of the second tree is 35.52 m

Problem 2 :

A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30° . Calculate the distance of the hill from the ship and the height of the hill. (√3 = 1.732)

Solution :

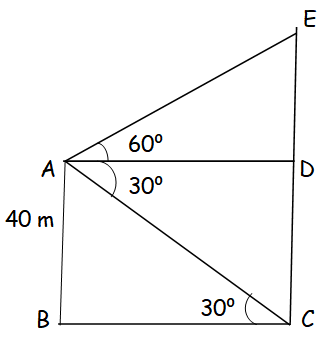
In triangle AED,

tan 60  =  ED/AD

√3  =  ED/AD 

AD  =  ED/√3 -----(1)

In triangle ABC,

tan 30  =  AB/BC

1/√3  =  40/BC

BC  =  40√3  -----(2)

BC  =  AD

(1)  =  (2)

40√3  =  ED/√3

ED  =  40√3(√3) 

  =  40(3)

ED  =  120 m

Height of hill  =  ED + DC 

  =  120 + 40

  =  160 m

Distance from hill to ship  =  40√3

=  40(1.732)

=  69.28 m

Problem 3 :

If the angle of elevation of a cloud from a point ‘h’ meters above a lake is θ₁ and the angle of depression of its reflection in the lake is θ₂ . Prove that the height that the cloud is located from the ground is h(tan θ₁+ tan θ₂)/(tan θ₂ - tan θ₁)

Solution :

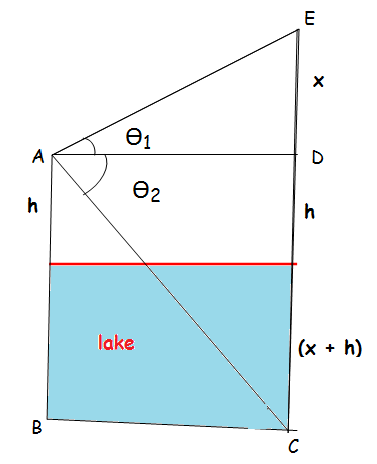
In triangle AED,

tan θ₁  =  ED/AD

tan θ₁  =  x/AD

AD  =  x/tan θ₁

AD  =  x cot θ₁  -----(1)

In triangle ADC,

tan θ₂  =  DC/AD

tan θ₂  =  (2h + x)/AD

AD  =  (2h + x)/tan θ₂

AD  =  (2h + x)cot θ₂ -----(2)

(1) = (2)

x cot θ_{1  =}  (2h + x)cot θ₂ 

x cot θ₁  =  2h cot θ₂ + x cot θ₂

x (cot θ₁ - cot θ₂) =  2h cot θ₂

x (tan θ₂ - tan θ₁)/(tan θ₁ tan θ₂) =  2h (1/tan θ₂)

2h  =  [xtan θ₂(tan θ₂ - tan θ₁)]/(tan θ₁ tan θ₂)

2h  =  x(tan θ₂ - tan θ₁)/tan θ₁

x  =  2h tan θ₁/(tan θ₂ - tan θ₁)

height of cloud  =  x + h

  =  [2h tan θ₁/(tan θ₂ - tan θ₁)] + h

  =  [2h tan θ₁+ h(tan θ₂ - tan θ₁)]/(tan θ₂ - tan θ₁)] 

  =  h[tan θ₁+ tan θ₂]/(tan θ₂ - tan θ₁)]

Hence proved.

Problem 4 :

An observation balloon is attached to the ground at point A. on a level with A and in the same straight line, the points B and C were chosen so that BC equals 100 meters. From the points B and C, the angle of elevation of the balloon is 40º and 30º respectively. Find the height of the balloon.

Solution :

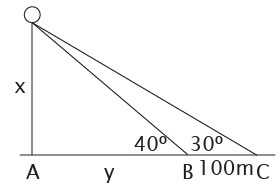
tan 40 = x/y

x = y tan 40 ----------(1)

tan 30 = x/(y + 100)

x = (y + 100) tan 30

x = (y + 100) (1/√3)

x = (y + 100)/√3 ----------(2)

(1) = (2)

y tan 40 = (y + 100)/√3

√3 (0.839)y = y + 100

1.45y = y + 100

1.45y - y = 100

0.45y = 100

y = 100/0.45

y = 222.22

Applying the value of y, we get

x = y tan 40

x = 222.22(0.839)

x = 186.46 m

Problem 5 :

Tom wished to find the width of a river. He observed a tree directly across the river on the opposite bank. The angle of elevation to the top of the tree was 32º. Then Tom moved directly back from the bank 50 meters and found that the angle of elevation to the top of the tree was 21º. What is the width of the river?

Solution :

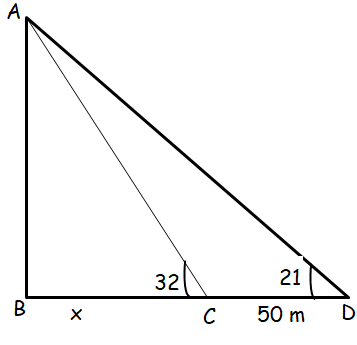
tan 32 = AB/BC

tan 32 = AB/x

0.624 = AB/x

AB = 0.624 x ------(1)

tan 32 = AB/BD

0.383 = AB/(x + 50)

AB = 0.383(x + 50) ------(2)

(1) = (2)

0.624x = 0.383(x + 50)

0.624x - 0.383x = 0.383(50)

0.241x = 19.15

x = 19.15/0.241

x = 79.46

Applying the value of x in (1), we get

AB = 0.624(79.46)

= 49.58

So, the height of the tree is 49.58 m and width of the river is 79.46 m

Problem 6 :

From a plane due to east at 265 m above sea level, the angles of depression of two ships sailing due east measure 35 and 25. How far apart are the ships ?

Solution :

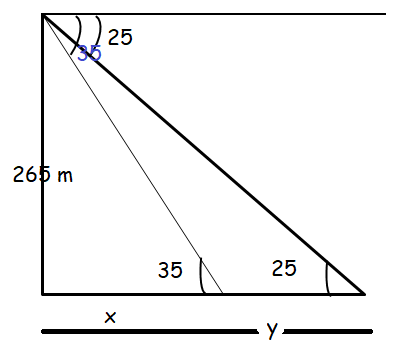
tan 35 = 265/x

x = 265/tan 35

x = 265/0.7

x = 378.5

tan 25 = 265/y

y = 265/tan 25

y = 265/0.466.

y = 568.6

y - x = 568.6 - 378.5

= 190.1

So, the distance between two ships is 190 m approximately.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.