PROBLEMS BASED ON PROPERTIES OF DISTANCE IN COORDINATE GEOMETRY

Problem 1 :

A (–1, 1), B (1, 3) and C (3, a) are points and if AB = BC, then find ‘a’.

Solution :

Distance between two points  =  √(x₂ - x₁)² + (y₂ - y₁)²

A (–1, 1) and B (1, 3)

  =  √(1+1)² + (3-1)²

  =  √2² + 2²

  =  √(4+4)

AB   =  √8

B (1, 3) and C (3, a)

  =  √(1-3)² + (3-a)²

  =  √(-2)² + (3-a)²

BC  =  √4 + (3-a)²

AB  =  BC

√8  =  √4 + (3-a)²

Taking squares on both sides

8  =  4 + (3-a)²

8  =  4 + 9 + a² - 6a

8  =  13 + a² - 6a

a² - 6a + 13 - 8  =  0

a² - 6a + 5  =  0

(a - 1)(a - 5)  =  0

a  =  1 and a  =  5

Problem 2 :

The abscissa of a point A is equal to its ordinate, and its distance from the point B(1, 3) is 10 units, What are the coordinates of A?

Solution :

Since the point A is equal to its ordinates

x  =  y

Let A(x, x)

Distance between the points A and B :

A(x, x)  B(1, 3)

√(1-x)² + (3-x)²  =  10

Taking squares on both sides

(1-x)² + (3-x)²  =  100

1 - 2x + x² + 9 - 6x + x²  =  100

2x² - 8x + 10 - 100  =  0

2x² - 8x - 90  =  0

Divide the entire equation by 2, we get

x² - 4x - 45  =  0

(x - 9)(x + 5)  =  0

x  =  9 and x  =  -5

A(9, 9) or B(-5, -5)

Problem 3 :

The point (x, y) is equidistant from the points (3, 4) and

(–5,6). Find a relation between x and y.

Solution :

Let the points be p (x, y) A(3, 4) and B(-5, 6)

PA  =  PB

√(3-x)² + (4-y)²   =  √(-5-x)² + (6-y)² 

Taking squares on both sides

(3-x)² + (4-y)²   =  (5+x)² + (6-y)² 

9 - 6x + x² + 16 - 8y + y²  =  25 + 10x + x² + 36 - 12y + y²

-6x - 10x - 8y + 12y  + 25 - 61 =  0

-16x + 4y - 36 =  0

4x - y + 9  =  0

y  =  4x + 9

Problem 4 :

Let A(2, 3) and B(2, –4) be two points. If P lies on the x-axis, such that AP = (3/7)AB, find the coordinates of P.

Solution :

Since the point P lies on x-axis, the y-coordinate will be 0.

A(2, 3) P(x, 0)

  =  √(x - 2)² + (0 - 3)²  

  =  √(x - 2)² + 9  ------(1)

A(2, 3) B(2, -4)

  =  √(2 - 2)² + (-4 - 3)²  

  =  √0² + (-7)² 

  =  7 ------(2)

AP = (3/7)AB

√(x - 2)² + 9   =  (3/7) 7

(x - 2)² + 9   =  3²

x² - 4x + 4 + 9 - 9  =  0

x² - 4x + 4  =  0

(x - 2) (x - 2)  =  0

x  =  2 and x  =  2

Hence the point P is (2, 0)

Problem 5 :

Show that the point (11, 2) is the center of the circle passing through the points (1, 2), (3, –4) and (5, –6)

Solution :

Let the center point be O (11, 2)

A(1, 2) B(3, -4) and C(5, -6)

AO  =  BO  =  CO  

O (11, 2) and A(1, 2)

=  √(1 - 11)² + (1 - 11)²

=  √100 + 100

=  √200

O (11, 2) and B(3, -4)

=  √(3 - 11)² + (-4 - 2)²

=  √(-8)² + (-6)²

=  √64 + 36

=  √100

O (11, 2) and C (5, –6)

=  √(5 - 11)² + (-6 - 2)²

=  √(-6)² + (-8)²

=  √36 + 64

=  √100

Hence the given point (11, 2) is the center of the circle.

Problem 6 :

The radius of a circle with center at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points.

Solution :

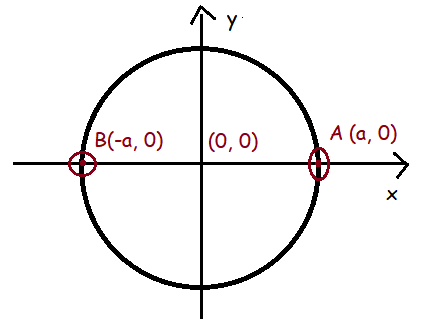
From the diagram given above, we come to know that the distance between the points (0, 0) and (a, 0) is 30 units.

√(0 - a)² + (0 - 0)²  =  30

√(-a)²  =  30

a  =  30 

it is clearly shown that circle intersects the co-ordinate axes at four points. and that are (30, 0), (-30, 0), (0, 30) and (0, -30). 

now, distance between (30,0) and (0,30)

=  √[(30 - 0)² + (0 - 30)²]

=  √[30² + 30²]

=  √[900 + 900]

=  √1800

=  30√2 units 

Similarly , you can find distance between any such two points. 

for better understanding, let

A  =  (30, 0)

B  =  (0, 30)

C  =  (-30, 0)

D  =  (0, -30) 

Then,

AB  =  BC  =  CD  =  DA  =  30√2 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.