PROBLEMS BASED ON CIRCLES EXAMPLES

About "Problems Based on Circles Examples"

Problems Based on Circles Examples :

Here we are going to see some example problems based on circles.

Problems Based on Circles Examples - Practice questions

Question 1 :

Th e diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre.

Solution :

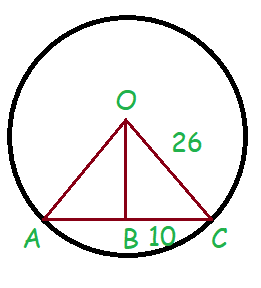
Diameter  =  52 cm

Radius of circle  =  26 cm

In triangle BOC,

OC²  =  OB² + BC²

26²  =  OB² + 10²

676 - 100  =  OB²

OB  =  √576

OB  =  24

Question 2 :

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle

Solution : 

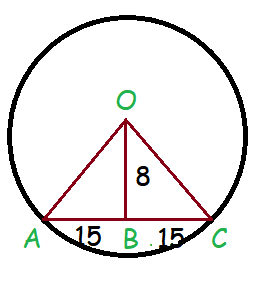
In triangle BOC,

OC²  =  OB² + BC²

OC²  =  8² + 15²

OC²  =  64 +  225

OC  =  √289

OC  =  17

Question 3 :

Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 4√2 cm and also find <OAC and <OCA.

Solution :

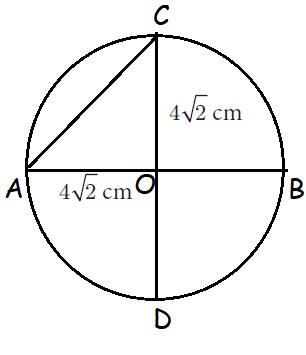
AC²  =  AO² + CO²

AC²  =  (4√2)² + (4√2)²

AC²  =  16(2) + 16(2)

AC²  =  64

AC  =  √64

AC  =  8 cm 

In triangle AOC,

<COA  =  90

OC  =  OA  

Equal sides will form a equal angles.

<OCA  =  <OBC

Question 4 :

A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord.

Solution : 

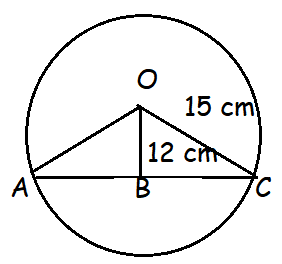
Let BC  =  x 

OC²  =  OB² + BC²

15²  =  12² + x²

225  -  144  =  x²

x  =  √81

x  =  9 cm 

AC  =  2BC  =  2(9)  =  18 cm

Question 5 :

In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?

Solution :

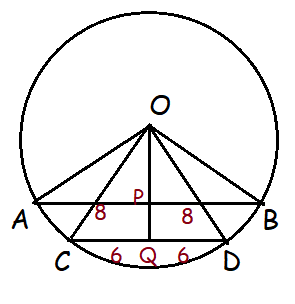
In triangle OPB,

OB²  =  OP² + PB²

OA  =  OB  =  OC  =  OD  =  10 (Radius)

10²  =  OP² + 8²

OP²  =  100 - 64

OP²  =  36

OP  =  √36

OP  =  6 cm

In triangle OQD,

OD²  =  OQ² + QD²

10²  =  OQ² + 6²

OQ²  =  100 - 36

OQ²  =  64

OQ  =  √64

OQ  =  8 cm

Distance between two chords  PQ  =  OQ - OP

  =  8 - 6

=  2 cm

Question 6 :

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.

Solution :

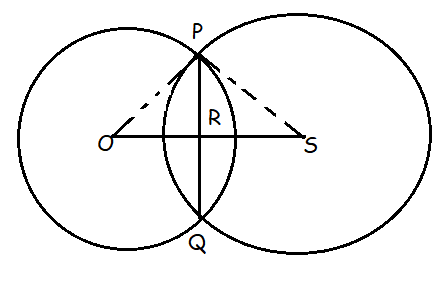
OP  =  3 cm, PS  =  5 cm and OS  =  4 cm

Let RS be x

OR  =  4 - x

In triangle POR,

OP²  =  OR² + PR²

3²  =  x² + PR²

PR²  =  9 - x²   ------(1)

In triangle PRS,

PS²  =  PR² + RS²

5²  =  PR² + (4 - x)²

PR²  =  25 - (4 - x)²

PR²  =  25 - (16 - 8x + x²)

PR²  =  25 - 16 + 8x - x²

PR²  =  9 + 8x - x²  ----(2)

(1)  =  (2)

9 - x²  =  9 + 8x - x²  

8x  =  0

x  =  0

By applying the value of x in (1), we get

PR²  =  9 - 0

PR²  =  9  ==>  PR  =  3

PQ  =  2PR

PQ  =  2(3)

PQ  =  6 cm

After having gone through the stuff given above, we hope that the students would have understood, "Problems Based on Circles Examples"

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.