PROBLEM SOLVING IN GEOMETRY WITH PROPORTIONS

Properties of Proportions

1. Cross Product Property :

The product of the extremes equals the product of the means.

If a/b = c/d, then ad = bc.

2. Reciprocal Property :

If two ratios are equal, then their reciprocals are also equal.

If a/b = c/d, then b/a = d/c.

3. Alternendo Property :

If a/b = c/d, then a/c = b/d.

4. Componendo Property :

If a/b = c/d, then (a + b)/b = (c + d)/d.

Using Properties of Proportions

Example 1 :

Say, whether the statement given below is true.

If x/4 = y/16, then x/y = 1/4.

Solution :

Given :

x/4 = y/16

Using Alternendo Property,

x/y = 4/16

Simplify.

x/y = 1/4

Hence, the statement is true.

Example 2 :

Say, whether the statement given below is true.

If p/3 = q/5, then (p + 3)/3 = (q + 3)/5

Solution :

Given :

p/3 = q/5

Using Componendo Property,

(p + 3)/3 = (q + 5)/5

Because (p + 3)/3 ≠ (q + 3)/5, the conclusions are equivalent.

Hence, the statement is false.

Example 3 :

In the diagram shown below,

PQ/QS = PR/RT

Find the length of QS.

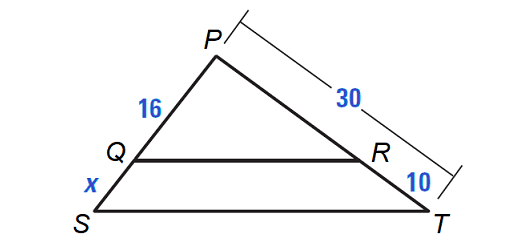
Solution :

Given :

PQ/QS = PR/RT

Substitute.

16/x = (30 - 10)/10

Simplify.

16/x = 20/10

16/x = 2/1

By reciprocal property, we have

x/16 = 1/2

Multiply each side by 16.

16 ⋅ (x/16) = (1/2) ⋅ 16

Simplify.

x = 8

Hence, the length of BD is 8 units.

Geometric Mean

The geometric mean of two positive numbers a and b is the positive number x such that

a/x = x/b

If we solve this proportion for x, we find that

x = √(a ⋅ b)

which is a positive number.

For example, the geometric mean of 8 and 18 is 12.

Because 8/12 = 12/18 and also because

√(8 ⋅ 18) = √144 = 12

Using Geometric Mean

Example 4 :

International standard paper sizes are commonly used all over the world. The various sizes all have the same width-to-length ratios. Two sizes of paper are shown below, called A4 and A3. The distance labeled x is the geometric mean of 210 mm and 420 mm. Find the value of x.

Solution :

Using the given information, write proportion.

210/x = x/420

Using cross product property,

x² = 210 ⋅ 420

Take radical on both sides.

√x² = √(210 ⋅ 420)

Simplify.

x = √(210 ⋅ 210 ⋅ 2)

x = 210√2

The geometric mean of 210 and 420 is 210√2, or about 297.

Hence, the distance labeled x in the diagram is about 297 mm.

Using Proportions in Real Life

Example 5 :

A scale model of the Titanic is 107.5 inches long and 11.25 inches wide. The Titanic itself was 882.75 feet long. How wide was it?

Solution :

One way to solve this problem is to set up a proportion that compares the measurements of the Titanic to the measurements of the scale model.

Problem Solving Strategy :

Multiply each side by 11.25.

11.25 ⋅ (x/11.25) = (882.75/107.5) ⋅ 11.25

Simplify.

x = (882.75 ⋅ 11.25) / 107.5

Using calculator, we have

x ≈ 92.4

Hence, the Titanic was about 92.4 feet wide.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.