PROBABILITY PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
A coin is tossed three times. What is the probability of getting :
(i) 2 heads
(ii) at least 2 heads
Solution :
When a coin is tossed three times, first we need enumerate all the elementary events.
This can be done using 'Tree diagram' as shown below :

So, the elementary events are HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
That is,
S = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }
Thus, the number of elementary events n(s) = 8.
(i) 2 heads :
Out of these 8 outcomes, 2 heads occur in three cases namely HHT, HTH and THH.
If we denote the occurrence of 2 heads by the event A and if assume that the coin as well as performer of the experiment is unbiased then this assumption ensures that all the eight elementary events are equally likely.
Then by the classical definition of probability, we have
P(A) = n(A) / n(s)
P(A) = 3/8
P(A) 0.375 or 37.5%
(ii) at least 2 heads :
Let B denote occurrence of at least 2 heads i.e. 2 heads or 3 heads.
Since 2 heads occur in 3 cases and 3 heads occur in only 1 case, B occurs in 3 + 1 or 4 cases.
By the classical definition of probability,
P(B) = 4/8
P(B) = 0.50 or 50%
Problem 2 :
A dice is rolled twice. What is the probability of getting a difference of 2 points?
Solution :
If an experiment results in p outcomes and if the experiment is repeated q times, then the total number of outcomes is pq.
In the present case, since a dice results in 6 outcomes and the dice is rolled twice, total no. of outcomes or elementary events is 62 or 36.
We assume that the dice is unbiased which ensures that all these 36 elementary events are equally likely.
Now a difference of 2 points in the uppermost faces of the dice thrown twice can occur in the following cases :
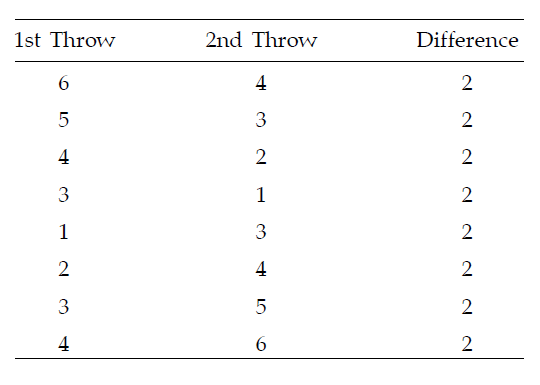
Thus denoting the event of getting a difference of 2 points by A, we find that the no. of outcomes favorable to A, from the above table, is 8.
By classical definition of probability, we get
P(A) = 8/36
P(A) = 2/9
Problem 3 :
Two dice are thrown simultaneously. Find the probability that the sum of points on the two dice would be 7 or more.
Solution :
If two dice are thrown then, as explained in the last problem, total no. of elementary events is 62 or 36.
Now a total of 7 or more i.e. 7 or 8 or 9 or 10 or 11 or 12 can occur only in the following combinations :
Sum = 7 -----> (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
Sum = 8 -----> (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
Sum = 9 -----> (3, 6), (4, 5), (5, 4), (6, 3)
Sum = 10 -----> ((4, 6), (5, 5), (6, 4)
Sum = 11 -----> (5, 6), (6, 5)
Sum = 12 -----> (6, 6)
Thus the no. of favorable outcomes is 21. Letting A stand for getting a total of 7 points or more, we have
P(A) = 21/36
P(A) = 7/12
Problem 4 :
What is the chance of picking a spade or an ace not of spade from a pack of 52 cards?
Solution :
A pack of 52 cards contain 13 Spades, 13 Hearts, 13 Clubs and 13 Diamonds.
Each of these groups of 13 cards has an ace.
Hence the total number of elementary events is 52 out of which 13 + 3 or 16 are favorable to the event A representing picking a Spade or an ace not of Spade.
Thus we have
P(A) = 16/52
P(A) = 4/13
Problem 5 :
Find the probability that a four digit number comprising the digits 2, 5, 6 and 7 would be divisible by 4.
Solution :
Since there are four digits, all distinct, the total number of four digit numbers that can be formed without any restriction is 4! or 4 × 3 × 2 × 1 or 24.
Now a four digit number would be divisible by 4 if the number formed by the last two digits is divisible by 4.
This could happen when the four digit number ends with 52 or 56 or 72 or 76.
If we fix the last two digits by 52, and then the 1st two places of the four digit number can be filled up using the remaining 2 digits in 2! or 2 ways.
That is,
6752
7652
Thus there are 2 four digit numbers that end with 52.
Proceeding in this manner, we find that the number of four digit numbers that are divisible by 4 is 4 × 2 or 8.
If A denotes the event that any four digit number using the given digits would be divisible by 4, then we have
P(A) = 8 / 24
P(A) = 1 / 3
Problem 6 :
A committee of 7 members is to be formed from a group comprising 8 gentlemen and 5 ladies. What is the probability that the committee would comprise :
(a) 2 ladies,
(b) at least 2 ladies.
Solution :
Since there are altogether 8 + 5 or 13 persons, a committee comprising 7 members can be formed in
13C7 = 13C6 = (13x12x11x10x9x8) / (6x5x4x3x2x1)
13C7 = 11x12x13
13C7 = 429
(a) 2 ladies :
When the committee is formed taking 2 ladies out of 5 ladies, the remaining (7–2) or 5 committee members are to be selected from 8 gentlemen.
Now 2 out of 5 ladies can be selected in 5C2 ways and 5 out of 8 gentlemen can be selected in 8C5 ways.
Thus if A denotes the event of having the committee with 2 ladies, then A can occur in 5C2 x 8C5 ways
5C2 x 8C5 = 5C2 x 8C3
5C2 x 8C5 = 10 x 56
5C2 x 8C5 = 560
Hence, P(A) = 560 / 1716 = 140 / 429
(b) at least 2 ladies :
Since the minimum number of ladies is 2, we can have the following combinations :

Thus if B denotes the event of having at least two ladies in the committee, then B can occur in
= (5C2 × 8C5) + (5C3 × 8C4) + (5C4 × 8C3) + (5C5 × 8C2)
= 1568 ways
So,
P(B) = 1568/1716
P(B) = 392/429
Problem 7 :
A point is chosen at random inside the circle having a diameter of 8 inches. What is the probability that the point is at least 1.5 inches away from the center of the circle ?
Solution :
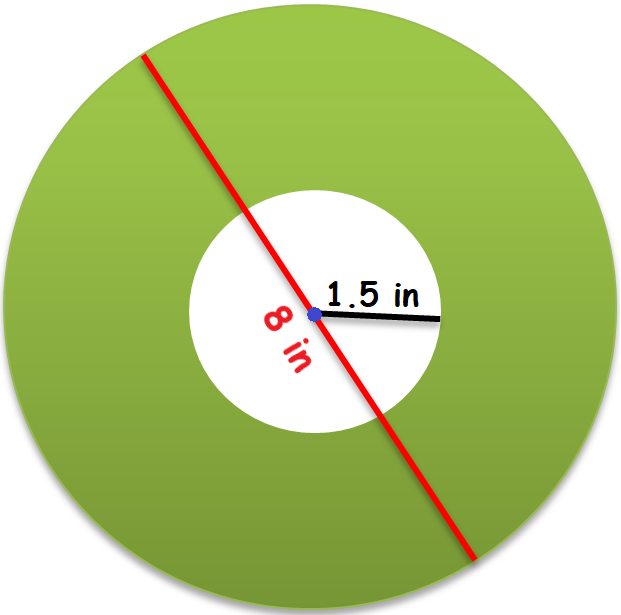
According to the question, we have to find the probability for the point to be in the green region of the above diagram.
Then, the required probability is
= Area of the green region / Area of the larger circle
Area of the Larger Circle :
= πr2
Here,
radius (r) = diameter/2 = 8/2 = 4 inches
Then,
= π(4)2
= 16π square inches
Area of the Green Region :
= Area of the larger circle - Area of the smaller circle
= π(4)2 - π(1.5)2
= 16π - 2.25π
= 13.75π square inches
Required Probability :
= Area of the green region / Area of the larger circle
= 13.75π / 16π
≈ 0.86
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 2)
Feb 19, 26 07:14 PM
Digital SAT Math Problems and Solutions (Part - 2) -
Tricky SAT Math Problems Solved Easily
Feb 19, 26 09:11 AM
Tricky SAT Math Problems Solved Easily -
Digital SAT Math Problems and Solutions (Part - 1)
Feb 18, 26 03:01 AM
Digital SAT Math Problems and Solutions (Part - 1)