PRINCIPAL VALUE OF TRIGONOMETRIC FUNCTIONS

Principal Solution :

The solution in which the absolute value of the angle is the least is called principal solution.

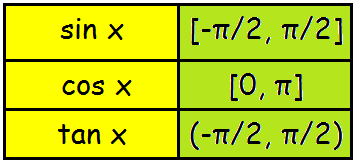
For example the value of cos o° is 1, the value of cos 2π, 4π ,...... are also 1. But the 0 is known as principal value.

Example 1 :

Find the principal value of the following

cos x  =  √3/2

Solution :

cos x  =  √3/2 > 0

Principal value of x must be in [0, π]. Since cos x is positive the principal value is in the first quadrant.

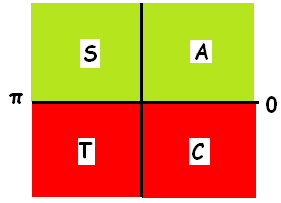
We have to think about the angle of cos for which we get the value √3/2.

cos  π/6  =  √3/2 and π/6 ∈ [0, π]

Hence the principal value of x is π/6.

Example 2 :

Find the principal value of the following

cos θ  =  - √3/2

Solution :

cos θ  =  - √3/2 < 0

Whenever we have cos θ the principal value of θ must be in [0, π].  We have to choose one of the angles from the first or second quadrant.

Since the value of cos θ is negative, we have to choose the angle from the second quadrant. For that we have to think about the angle of cos for which we get the value √3/2. 

cos (π - (π/6)) = cos 5π/6

cos  5π/6  =  -√3/2

Hence the principal value of θ is 5π/6.

Example 3 :

Find the principal value of the following

cosec θ  =  -2/√3

Solution :

cosec θ  =  -2/√3

sin θ  =  -√3/2 < 0 

θ lies in the third or fourth quadrant. But principal value must be in [-π/2, π/2]

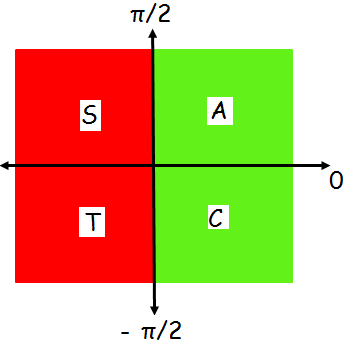
In the first quadrant we get only we get positive values for all trigonometric ratios.So we have to choose one of the angles from 0 to -π/2 that is negative angle.

Now we have to think about the angle of sin for which we get the value √3/2.

sin (-π/3)  =  -√3/2

Hence the principal value of θ is -π/3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.