PRIME AND COMPOSITE NUMBERS

Think about the situation :

The teacher gave 5 buttons to David and 6 buttons to Lily and asked them to arrange the buttons in all possible rows in such a way that the number of buttons in each row is equal. They did it, in different ways as shown below :

David's Ways

By arranging 5 buttons in a row, he gets 1 row. 

1 x 5  =  5

By arranging 1 button in each row, he gets 5 rows. 

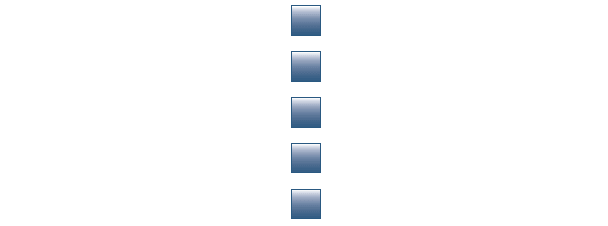
5 x 1  =  5

He realizes that 5 buttons can be arranged in only 2 rectangular ways. Hence, the only factors of 5 are 1 and 5 (number of rows).

Lily's Ways

By arranging 6 buttons in a row, she gets 1 row. 

1 x 6  =  6

By arranging 3 buttons in each row, she gets 2 rows.

2 x 3  =  6

By arranging 2 buttons in each row, she gets 3 rows. 

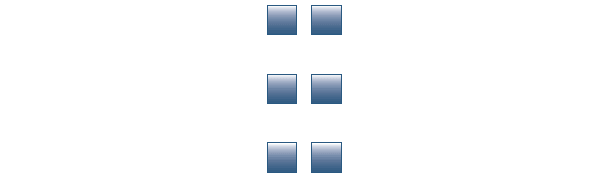
3 x 2  =  6

By arranging 1 button in each row, she gets 6 rows. 

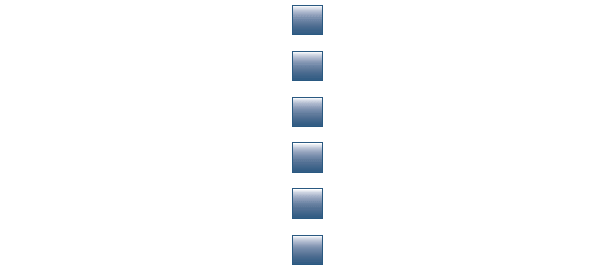
6 x 1  =  6

She realizes that 6 buttons can be arranged in 4 rectangular ways. Hence, the factors of 6 are 1, 2, 3 and 6 (number of rows).

●Make different rectangular arrangements using 1 button, 2 buttons, 3 buttons, 4 buttons,…, 10 buttons and complete the following table :

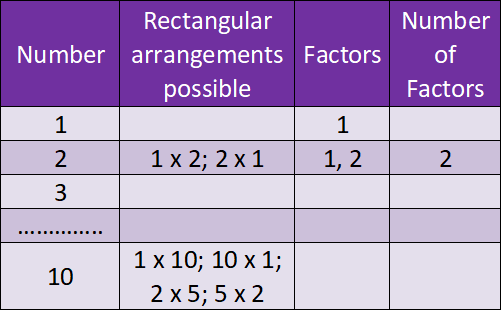
From the table, we conclude that

● A natural number greater than 1, having only two factors namely 1 and the number itself, is called a prime number.

For example, 2 (1 x 2) is a prime number as is 13 (1 x 13).

● A natural number having more than 2 factors is called composite number. 

For example, 15 is a composite number (15 = 1 x 3 x 5) as is 70 (1 x 2 x 5 x 7).

Perfect Number

A number is a perfect number if the sum of its factors other than the given number gives the same number.

For example, 6 is a perfect number, since adding the factors of 6 (other than 6), namely 1, 2 and 3 gives the given  number 6.

That is, 1 + 2 + 3  =  6 is the given number.

Check whether 28, 54 and 496 are perfect numbers or not.

Co-Primes or Relatively Prime

If the greatest common factor (GCF) of two numbers is 1, then the numbers are said to be co-primes or relatively prime or mutually prime.

Here, the two numbers can both be primes as (3, 11) or both can be composites as (16, 35) or one can be a prime and other a composite as (7, 14).

Activity

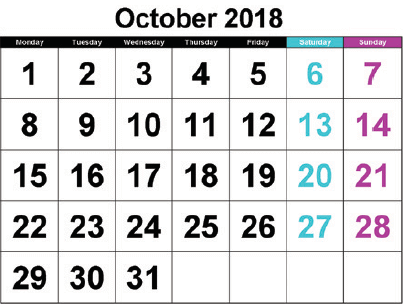
(i) List out the prime and composite numbers represented by the dates in the month of October.

(ii) Generate a few composite numbers by product of two or more natural numbers.

(iii) Classify the numbers 34, 57, 71, 93, 101, 111 and 291 as prime or composite.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.