PREDICTING WITH LINEAR EQUATIONS

We can use an equation of a linear relationship to predict a value between data points that we already know.

In most of the cases, we use slope-intercept form equation to make predictions. 

Example 1 : 

The graph shows the cost for taxi rides of different distances. Predict the cost of a taxi ride that covers a distance of 6.5 miles.

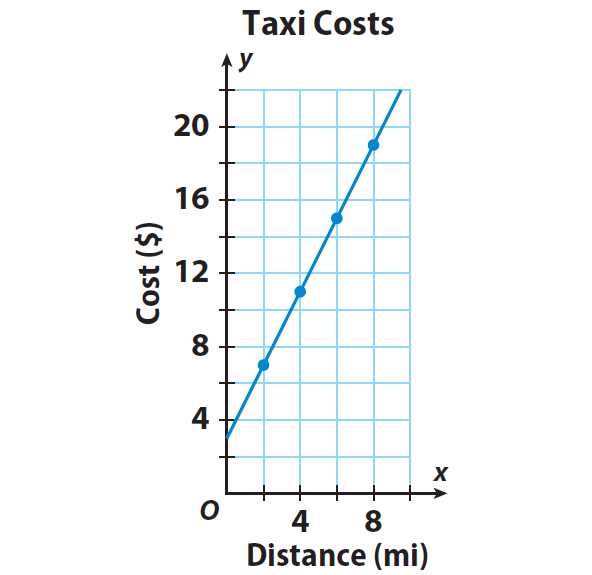
Solution : 

Since we want to predict the cost of a taxi ride, the appropriate linear equation for the given situation is slope-intercept form (y = mx + b), assuming "y" as the cost of a taxi ride and "x" as distance. 

Step 1 : 

Write the equation of the linear relationship.

Choose any two points in the form (x, y), from the graph to find the slope :

For example, let us choose (2, 7) and (4, 11).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute :

(x₁, y₁)  =  (2, 7)

(x₂, y₂)  =  (4, 11)

Then, 

m  =  (11 - 7) / (4 - 2)

m  =  4 / 2

m  =  2

Step 3 : 

Find the y-intercept using the slope and any point from the table.

Slope-intercept form equation of a line :

y  =  mx + b

Substitute  m  =  2, and (x, y)  =  (2, 7). 

7  =  2(2) + b

7  =  4 + b

3  =  b

Step 4 : 

Now, substitute  m = 2 and b = 3 in slope-intercept form equation of a line.

y  =  mx + b

y  =  2x + 3

Step 5 : 

Predict the cost of a taxi ride that covers a distance of 6.5 miles.

Substitute x = 6.5 in the equation y = 2x + 3. 

y  =  2(6.5) + 3

y  =  13 + 3

y  =  16

So, the cost of a taxi ride that covers a distance of 6.5 miles is $16.

Example 2 : 

The table shows the temperature of a fish tank during an experiment. Write the appropriate linear equation for the given situation and use the equation to predict the temperature at the 7th hour.

Solution : 

Step 1 : 

Notice that the change in the temperature is the same for each increase of 1 hour in time. So, the relationship is linear.

Since we want to find the temperature at the 7th hour, the appropriate linear equation for the given situation is slope-intercept form (y = mx + b), assuming "y" as temperature and "x" as hours.  

Step 2 : 

Choose any two points in the form (x, y), from the table to find the slope :

For example, let us choose (0, 82) and (1, 80).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute :

(x₁, y₁)  =  (2, 7)

(x₂, y₂)  =  (4, 11)

Then, 

m  =  (80 - 82) / (1 - 0)

m  =  -2 / 1

m  =  -2

Step 3 : 

Find the y-intercept using the slope and any point from the table.

Slope-intercept form equation of a line :

y  =  mx + b

Substitute m  =  -2, and (x, y)  =  (0, 82).

82  =  -2(0) + b

82  =  0 + b

82  =  b

Step 4 : 

Now, substitute m = -2 and b = 82 in slope-intercept form equation of a line.

y  =  mx + b

y  =  -2x + 82

Step 5 : 

Predict the temperature at the 7th hour.

Substitute x = 7 in the equation y = -2x + 82. 

y  =  -2(7) + 82

y  =  -14 + 82

y  =  68

So, the temperature at the 7th hour is 68⁰ F.

Example 3 : 

Elizabeth’s cell phone plan lets her choose how many minutes are included each month. The table shows the plan’s monthly cost y for a given number of included minutes x. Write an equation in slope-intercept form to represent the situation and use it to predict cost of plan for 800 minutes included.

Solution : 

Step 1 : 

Notice that the change in cost is the same for each increase of 100 minutes. So, the relationship is linear.

Step 2 : 

Choose any two points in the form (x, y), from the table to find the slope :

For example, let us choose (100, 14) and (200, 20).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute :

(x₁, y₁)  =  (100, 14)

(x₂, y₂)  =  (200, 20)

Then, 

m  =  (20 - 14) / (200 - 100)

m  =  6 / 100

m  =  0.06

Step 3 : 

Find the y-intercept using the slope and any point from the table.

Slope-intercept form equation of a line :

y  =  mx + b

Substitute  m  =  0.06, and (x, y)  =  (100, 14).

14  =  0.06(100) + b

14  =  6 + b

8  =  b

Step 4 : 

Now, substitute m = 0.06 and b = 8 in slope-intercept form equation of a line.

y  =  mx + b

y  =  0.06x + 8

Step 5 : 

Predict cost of plan for 800 minutes included. 

Substitute x = 800 in the equation y = 0.06x + 8. 

y  =  0.06(800) + 8

y  =  48 + 8

y  =  56

So, the cost of plan for 800 minutes included is $56. 

Example 4 : 

The rent charged for space in an office building is a linear relationship related to the size of the space rented.At west main street office rentals, $750 rent charged for 600 square feet of space and $1150 rent charged for 900 square feet of space. Write an equation in slope-intercept form for the rent at West Main Street Office Rentals and use it to predict the rent for 1200 square feet of space.

Solution : 

Step 1 :

Identify the independent and dependent variables.

The independent variable (x) is the square footage of floor space.

The dependent variable (y) is the monthly rent.

Step 2 :

Write the information given in the problem as ordered pairs.

The rent for 600 square feet of floor space is $750 :

(600, 750)

The rent for 900 square feet of floor space is $1150 :

(900, 1150)

Step 3 : 

Find the slope.  

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute :

(x₁, y₁)  =  (600, 750)

(x₂, y₂)  =  (900, 1150)

Then, 

m  =  (1150 - 750) / (900 - 600)

m  =  400 / 300

m  =  4/3

Step 4 : 

Find the y-intercept.

Use the slope 4/3 and one of the ordered pairs (600, 750).

Slope-intercept form : 

y  =  mx + b

Substitute  m = 4/3,  x = 600 and y = 750.  

750  =  (4/3)(600) + b

750  =  (4)(200) + b

750  =  800 + b

-50  =  b

Step 5 : 

Substitute the slope and y-intercept.

Slope-intercept form

y  =  mx + b 

Substitute  m = 4/3 and b = -50.

y  =  (4/3)x + (-50)

y  =  (4/3)x - 50 

Step 6 : 

Predict the rent for 1200 square feet of space.

Substitute x = 1200 in the equation y = (4/3)x - 50.

y  =  (4/3)(1200) - 50

y  =  1600 - 50

y  =  1550

So, the rent for 1200 square feet of space is $1550. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.