PRE CALCULUS PROBLEMS AND SOLUTIONS
(Part - 9)

Problem 1 :

What does the Intermediate Value Theorem say about the function f(x) = x² + x + 4 on the interval?

A)  f(x) must have exactly one zero in the interval (0, 2).

B)  f(x) must have at least one zero in the interval (0, 2).

C)  f(x) must stay strictly -4 and 2 on the interval (0, 2).

D)  Nothing, because f(x) is not conitnuous on the interval [0, 2].

E)  Nothing, because f(0) = f(2).

Solution :

Problem 2 :

Is the function continuous at x = 3?

Solution :

Problem 3 :

Range : 2 ≤ y ≤ 8

y = a sin x + b

In the function above, change the values of a and b so that the graph fits tightly within the given range.

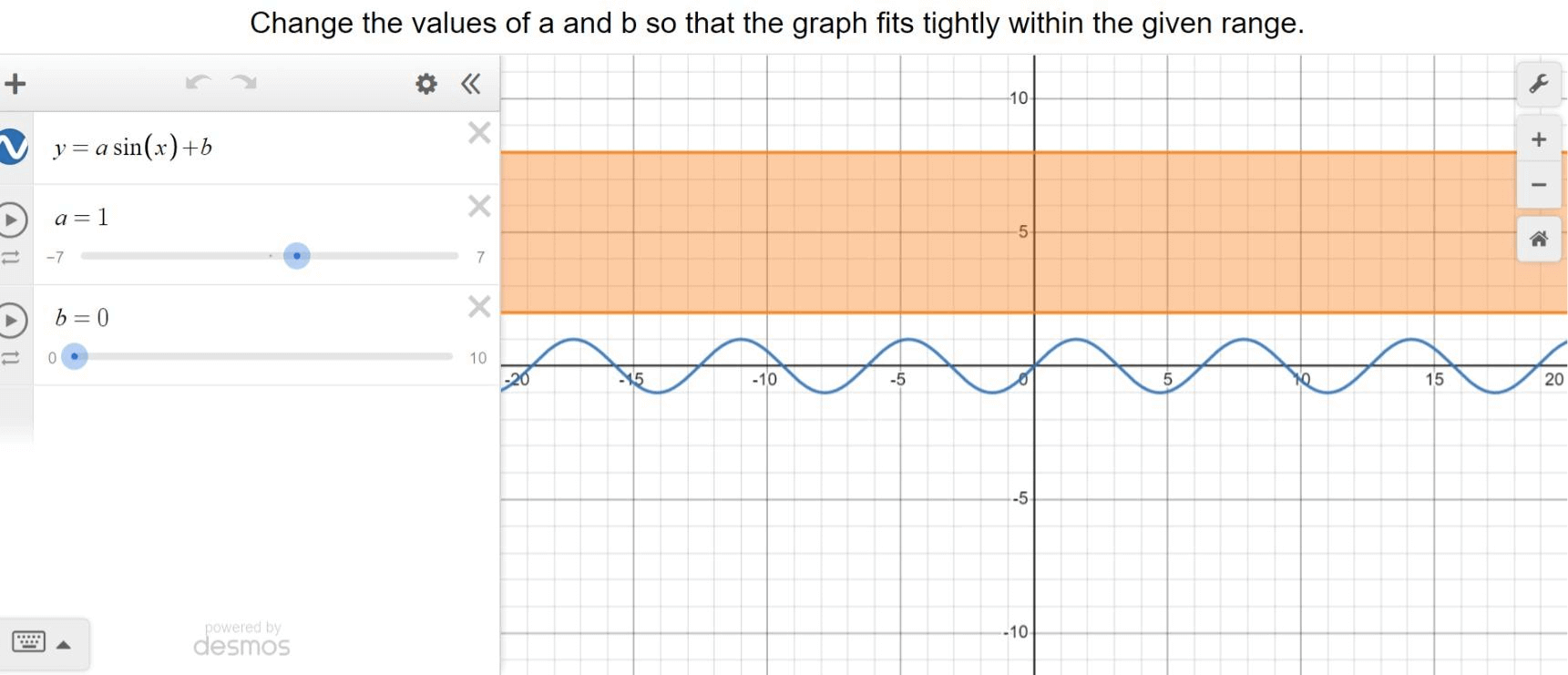
Solution :

Problem 4 :

A)  0

B)  Does not exist

C)  4

D)  1

E)  3

Solution :

Problem 5 :

Determine the limit.

A)  1

B)  0

C)  ∞

D)  -∞

E)  -1

Solution :

You might like these

Pre-Calculus Problems and Solutions (Part - 1)

Pre-Calculus Problems and Solutions (Part - 2)

Pre-Calculus Problems and Solutions (Part - 3)

Pre-Calculus Problems and Solutions (Part - 4)

Pre-Calculus Problems and Solutions (Part - 5)

Pre-Calculus Problems and Solutions (Part - 6)

Pre-Calculus Problems and Solutions (Part - 7)

Pre-Calculus Problems and Solutions (Part - 8)

Pre-Calculus Problems and Solutions (Part - 9)

Pre-Calculus Problems and Solutions (Part - 10)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.