AP Precalculus Problems and Solutions

Problem 1 :

Which of the following is equal to the above limit?

A)  1/6

B)  1/3

C)  3

D)  6

Solution :

Problem 2 :

The function h is given by h(x) = 8 ⋅ 2^x. For which of the following values of x, h(x) = 256?

A)  x = 2

B)  x = 5

C)  x = 8

D)  x = 16

Solution :

Problem 3 :

The function h is given by h(x) = log₃ x. Which of the following is equivalent to the expression

2 ⋅ h(w) + h(p),

where w and p are values in the domain of h?

A) log₃ (wp)²

B) (log₃ w)² ⋅ (log₃ p)

C) log₃ (w²p)

D) log₃ (2wp)

Solution :

Problem 4 :

Let x and y be positive constants. Which of the following is equivalent to 2ln x - 2 ln y ?

Solution :

Problem 5 :

The function f is given by f(x) = 2log₅ x. Which of the following describes f?

A) is an increasing function that increases at an increasing rate.

B) is an increasing function that increases at a decreasing rate.

C) is a decreasing function that decreases at an increasing rate.

D) is a decreasing function that decreases at a decreasing rate.

Solution :

Problem 6 :

The Richter scale is a numerical scale that uses base 10 logarithms for measuring an earthquake’s magnitude. The larger the number, the more intense the earthquake. As intensities increase multiplicatively by a factor of 10, the Richter scale increases additively by 1. Consider two earthquakes that occurred in the year 2022. An earthquake in Indonesia had a magnitude of 5.1, and an earthquake in Mexico had a magnitude of 2.5. Approximately how many times more intense was the Indonesia earthquake than the Mexico earthquake?

A)  2.6

B)  26

C)  100

D)  400

Solution :

Problem 7 :

The point P(3, 8) is on the graph of y = b^x, where b > 1.  The corresponding point P' on the graph of y + 3 = b^{x + 1} is

A)  (2, 11)

B)  (2, 5)

C)  (4, 11)

D)  (4, 5)

Solution :

Problem 8 :

The function y = f(x) has a domain of {x| 2 ≤ x ≤ 6, x ∈ R} and a range of {y| -4 ≤ y ≤ 8, y ∈ R}, The function undergoes the transformation y = -f(½x).

The domain and range of the transformed function are shown in row :

Solution :

Problem 9 :

The graph of y = f(x) is transformed into the graph of y = g(x), shown below.

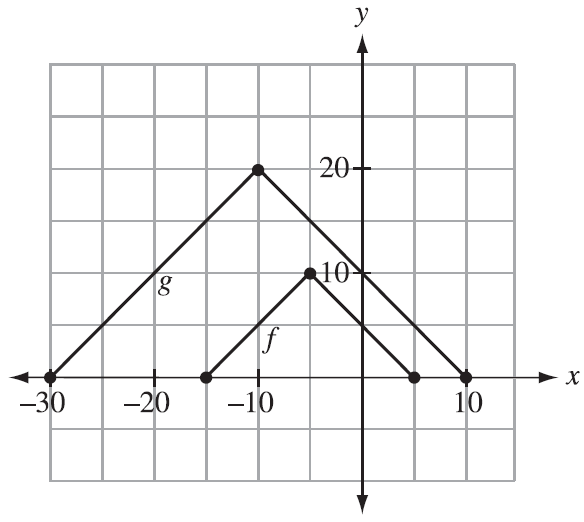
An equation for g(x) in terms of f(x) is

A)  g(x) = f(2x) + 10

B)  g(x) = f(½x) + 10

C)  g(x) = 2f(2x)

D)  g(x) = 2f(½x)

Solution :

Problem 10 :

The loudness of a sound is related to the logarithm of the ratio of the measured intensity, I, to a reference intensity, I₀. The loudness, L, of a sound is measured in decibels, dB, and can be determined using the following formula.

L = 10log₁₀(I/I₀)

During an international soccer tournament in 2010, a noisemaker called the vuvuzela had a measured loudness of 127 dB at full volume.

If the intensity of the sound of the vuvuzela is 5 000 times greater than the intensity of the sound of a lawn mower, then the measured loudness of the lawn mower, to the nearest decibel, is

A)  3 dB

B)  37 dB

C)  90 dB

D)  123 dB

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.