PRACTICE TEST FOR GRADE 10 MATH

Problem 1 :

Find the 5^th term of the Geometric progression

64, 16, 4………?

Solution :

a_n  =  a + (n - 1)d

a  =  64, d  =  16 - 64 ==> -48 and n  =  5 

a₅  =  64 + (5 - 1)(-48)

a₅  =  64 + 4(-48)

a₅  =  64 - 192

a₅  =  -128

So, the 5^th term of the given sequence is -128.

Problem 2 :

Find the sum of first 11 terms of the following A.P

3, 8, 13,……………...

Solution :

a  =  3, d  =  8 - 3 ==>  5 and n  =  11

S_n  =  (n/2) [2a + (n - 1)d]

S₁₁  =  (11/2) [2(3) + (11-1)5]

S₁₁  =  (11/2) [6 + 50]

S₁₁  =  (11/2) (56)

S₁₁  =  11 (28)

S₁₁  =  308

Problem 3 :

Find the sum of

11+12+13+………..+31

Solution :

Sum of natural numbers  =  n(n + 1)/2

11+12+13+………..+31  =  (1+2+3+ ..... +31) - (1+2+3+.....+10)

  =  31(32)/2 - 10(11)/2

  =  496 - 55

  =  441

So the sum of the given series is 441.

Problem 4 :

Find the total area of the squares whose sides are

20 cm, 21 cm ….........27 cm

respectively

Solution :

Total area of squares using side length are

20² + 21² + ........ + 27²

  =  (1²+2²+3²+.......+27²) - (1²+2²+3²+.......+19²)

Sum of squares  =  n(n + 1)(2n + 1)/6

=  (27⋅28⋅55)/6 - (19⋅20⋅39)/6 

=  6930 - 2470

=  4460

So the sum of total surface area of given squares is 4460 cm².

Problem 5 :

The radius of the top of a bucket is 18 cm and that of the bottom is 6 cm.Its depth is 24 cm.Find the capacity of the bucket.

Solution :

Volume of frustum cone  =  (1/3) π h (R² + r ² + R r)

R  =  18 cm, r  =  6 cm and height (h)  =  24 cm

  =  (1/3) (22/8) 24 [18² + 6 ² + 18(6)]

  =  22[324 + 36 + 108]

  =   10296 cm³

So, the capacity of the frustum cone is 10296 cm³.

Problem 6 :

A hemispherical bowl of radius 30 cm is filled with soap paste.If that paste is made into cylindrical soap cakes each of radius 5 cm and height 2 cm, how many cakes do we get?

Solution :

Radius of cylinder  =  5 cm and height of cylinder  =  2 cm

Volume of soap past filled in the hemispherical bowl

  =  n (Volume of one cylindrical soap cakes)

Radius of hemisphere  =  30 cm

Volume of soap paste in hemispherical bowl  =  (2/3)π r³

=  (2/3)π (30)³  ------(1)

Volume of one cylindrical soap  =  π r²h

=  π 5² (2) ------(2)

(1) / (2)

n  =  (2/3)π (30)³ / π 5² (2) 

n  =  360

So, the number of soaps made is 360.

Problem 7 :

If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} A = {2, 4, 6},B = {1, 2, 3, 5} find (AUB)’

Solution :

A u B  =  {1, 2, 3, 4, 5, 6}

(A u B)'  =  {7, 8, 9, 10}

Problem 8 :

In a class of 35 students 18 speak French,12 speak Hindi and 15 speak English.2 students speak French and Hindi.4 Hindi and English and 5 speak English and French. Calculate the number of students who speak all three languages.Also find the number of students Hindi and English but not French.

Solution :

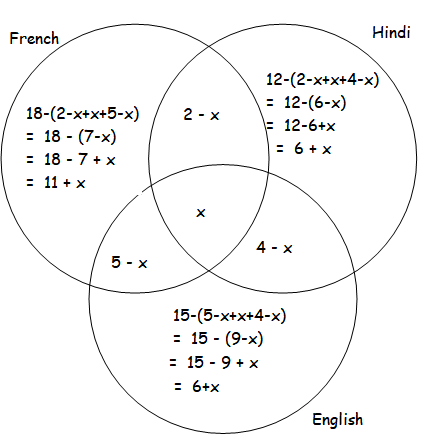
Total number of students  =  35

Number of students who speaks atleast one one language

11+x+2-x+6+x+x+5-x+4-x+6+x  =  35

34 + x  =  35

x  =  1

Number of students who speaks Hindi and English not French  =  4 - x

  =  4 - 1

  =  3

Problem 9 :

A bag contains ten, five and two dollar currencies. The total number of currencies is 20 and the total value of money is $125.If the second and third sorts of currencies are interchanged the value will be decreased by $6.Find the number of currency in each sort.

Solution :

Let x, y and z be the number of number of currencies in 10, 5 and 2 dollars respectively.

x+y+z  =  20  -----(1)

10x+5y+2z  =  125  -----(2)

10x+2y+5z  =  119  -----(3)

(1) ⋅ 10 ==>  10x+10y+10z  =  200

(1) - (2) ==> -10x-5y-2z  =  -125

                  -------------------------

                       5y+8z  =  75 ----(4)

(2)-(3)

10x+5y+2z  =  125

-10x-2y-5z  =  -119

------------------------

3y-3z  =  6

y-z  =  2 ----(5)

(4)+8(5) ==>  13y  =  75+16

                     13y  =  91

                       y  =  7

By applying the value of y in (5), we get

7-z  =  2

z  =  5

By applying the values of y and z in (1), we get

x + 7 + 5  =  20

x  =  20-12

x  =  8

So, the number of currencies in 5, 10 and 2 dollars are 8, 2 and 5 respectively.

Problem 10 :

Factories the cubic polynomial 

2x³  + x² - 5x + 2

Solution :

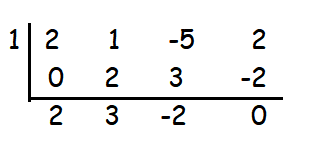
(x-1) is a factor. So, we can get the other two factors by factoring the quadratic polynomial.  

2x² + 3x - 2

(2x-1) (x+2)

So, the three factors are (2x-1) (x+2) and (x-1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.