PRACTICE QUESTIONS ON SET OPERATIONS ANSWERS

Question 1 :

From the given Venn diagram find

(i) A (ii) B (iii) A U B (iv) A n B

Also verify that n(A U B) = n(A) + n(B) - n(A n B)

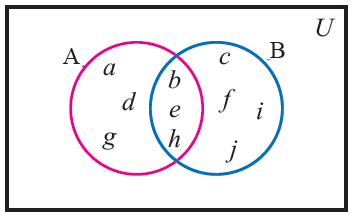
Solution :

The variables inside the circle A are known as elements of the set A.

A = { a, b, d, e, g, h }

The variables inside the circle B are known as elements of  the set B.

B = { b, c, e, f, i, j, h } 

The variables inside the circles A and B are known as elements of the set AUB.

A U B = { a, b, c, d, e, f, g, h, i, j } 

The variables in the common region of A and B are known as elements of A n B.

A n B = { b, e, h } 

To verify the given statement, we have to find the cardinal number of each set.

n (A)  =  6

n (B)  =  7

n (A U B)  =  10

n (A n B)  =  3

n(A U B) = n(A) + n(B) - n(A n B)

10  =  6 + 7 - 3

10  =  13 - 3

10  =  10

Hence it is proved.

Question 2 :

If n(U) = 38, n(A) = 16, n (AnB) = 12, n(B') = 20 find n(AUB) .

Solution :

n (A U B) = n (A) + n (B) - n (A n B)

n (B) = n (U) - n (B')

n (B) = 38 - 20  ==> 18

n (A U B) = n (A) + n (B) - n (A n B)

n (A U B) = 16 + 18 - 12

=  34 - 12

=  22

Hence the value of n (A U B) is 22.

Question 3 :

From the given Venn diagram find

(i) A (ii) B (iii) A U B (iv) A n B

Also verify that n(A U B) = n(A) + n(B) - n(A n B)

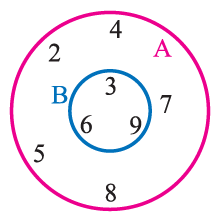
Solution :

The numbers inside the circle A are known as elements of set A.

A = { 2, 3, 4, 5, 6, 7, 8, 9 }

n (A)  =  8

The numbers inside the circle B are known as elements of set B.

B = { 3, 6, 9 }

n (B) = 3

The numbers inside the circles A and B are known as elements of the set AUB.

A U B = { 2, 3, 4, 5, 6, 7, 8, 9 }

n (A U B) = 8

The numbers in common region of A and B is known as elements of A n B.

A n B = {3, 6, 9}

n (A n B) = 3

n(A U B) = n(A) + n(B) - n(A n B)

8 = 8 + 3 - 3

8 = 8

Hence it is proved.

Question 4 :

From the venn diagram, write the elements of set A n B

Solution :

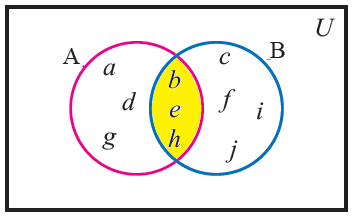
The variables in common region of A and B are known as elements of A n B.

A n B = { b, e, h } 

Question 5 :

If n(A) = 12, n(B) = 17 and n(A U B) = 21, find n(A n B)

Solution :

By using the formula,

n(A U B) = n (A) + n (B) - n (A n B)

we may find the value of n (A n B)

21  =  12 + 17 - n (A n B)

21  =  29 - n (A n B)

n (A n B)  =  29 - 21  ==>   8

Hence the value of n (A n B) is 8. 

Question 6 :

From the venn diagram, write the elements of the following sets

(i)  A'   (ii)  B'   (iii)  (A n B)'   (iv)  (A U B)'

Solution :

(i) A'

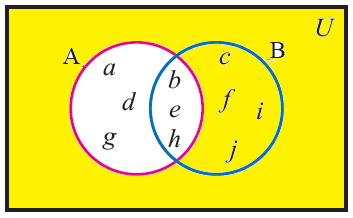
A' =  { c, f, i ,j }

(ii) B'

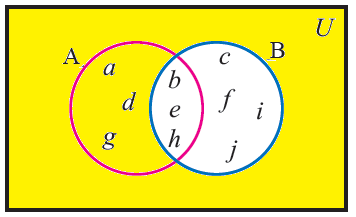
B' =  { a, d, g }

(iii) (A n B)'

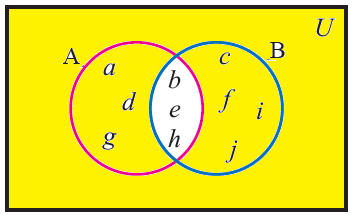
(A n B)'  =  { a, d, g, c, f, i, j }

(iv) (A U B)'

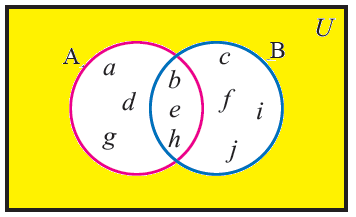
(A U B)'  =  {  }  (or) null set

Question 7 :

If n(U) = 43, n (A) =  26 find n (A')

Solution :

By using the formula,

n (A) + n (A')  =  n (U)

we may find the value of n (A')

26 + n (A') = 43

Subtract 26 on both sides

26 - 26 + n (A')  =  43 - 26

n (A')  =  17

Question 8 :

If n (U) = 38, n (A) = 16, n (A n B) = 12, n (B') = 20, find n (A U B).

Solution :

By using the formula,

n (B) + n (B')  =  n (U)

we may find the value of n (B')

n (B) + 20 = 38

Subtract 20 on both sides

n (B) + 20 - 20  =  38 - 20

n (B)  =  18

n (A U B) = n (A) + n (B) - n (A n B)

= 16 + 18 - 12

=  34 - 12

=  22

Question 9 :

If A = {- 2, - 1,0,3,4}, B = {- 1,3,5}, find (i) A - B (ii) B - A

Solution :

A = {- 2, - 1,0,3,4} and B = {- 1,3,5}

A - B = { -2, 0, 4}

B - A = { 5 }

Question 10 :

If A = {2, 3, 5, 7, 11} and B = {5, 7, 9, 11, 13} , find A Δ B.

Solution :

A = {2, 3, 5, 7, 11} and B = {5, 7, 9, 11, 13}

A - B = { 2, 3 }

B - A = { 9, 13 }

A Δ B = (A - B) U (B - A)

    =  { 2, 3, 9, 13 }

Question 11 :

Given that U = {3, 7, 9, 11, 15, 17, 18}, M = {3, 7, 9, 11} and N = {7, 11, 15, 17},

find (i) M - N    (ii) N - M     (iii) N' - M     (iv) M' - N

(v) M n (M - N)    (vi) N U (N - M)     (vii) n(M - N)

Solution :

U = { 3, 7, 9, 11, 15, 17, 18 }

M = { 3, 7, 9, 11 }

N = { 7, 11, 15, 17 }

(i) M - N 

The set M - N would contain the elements of the set M excluding the elements of M n N

M - N = { 3, 9 }

(ii) N - M 

The set N - M would contain the elements of the set M excluding the elements of N n M

N - M = { 15, 17 }

(iii) N' - M

N' = { 3, 9, 18 }

N' - M  =  {18} 

(iv) M' - N

M' = { 15, 17, 18 }

M' - N = { 18 }

(v) M n (M - N)

The set M n (M - N) would contain the set of common elements that we found in both the set M and (M - N)

M = { 3, 7, 9, 11 }  M - N = { 3, 9 }

M n (M - N)  =  { 3, 9}

(vi) N U (N - M)

N = { 7, 11, 15, 17 }    N - M = { 15, 17 }

N U (N - M)  =  {  7, 11, 15, 17 }

(vii) n(M - N)

Number of elements of set M - N is 2.

Hence  n(M - N) =  2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.