PRACTICE QUESTIONS ON RELATIONS AND FUNCTIONS

(1)  If the ordered pairs (x² − 3x, y² + 4y) and (-2,5) are equal, then find x and y.              Solution

(2)  The Cartesian product A×A has 9 elements among which (–1, 0) and (0,1) are found. Find the set A and the remaining elements of A × A.         Solution

(3)  Given that f(x)  =  

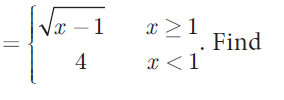
(i) f (0) (ii) f (3) (iii) f (a+1) in terms of a.(Given that a ≥  0)         Solution

(4)  Let A= {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A-> N be defined by f (n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.

Solution

(5)  Find the domain of the function f(x) =

Solution

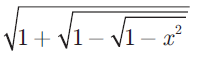
(6)  If f (x) = x² , g(x) = 3x and h(x) = x −2 , Prove that (f ∘ g) ∘ h = f ∘ (g ∘ h) .          Solution

(7)  Let A = {1, 2} and B = {1, 2, 3, 4} , C = {5, 6} and D = {5, 6 ,7, 8} . Verify whether A × C is a subset of B × D?       Solution

(8)  If f(x)  =  (x - 1)/(x + 1), x ≠ 1 show that f(f(x))  =  -1/x, provided x ≠ 0            Solution

(9)  The functions f and g are defined by f (x) = 6x + 8; g (x)  = (x - 2)/3

(i) Calculate the value of gg (1/2)

(ii) Write an expression for gf (x) in its simplest form.

Solution

(10)  Write the domain of the following real functions

(i) f (x)  =  (2x + 1)/(x - 9)

(ii)  p(x)  =  -5/(4x² + 1)

(iii)  g(x)  =  √(x - 2)

(iv) h(x)  =  x + 6     

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.