PRACTICE QUESTIONS ON RATIONAL NUMBERS FOR CLASS 8

Question 1 :

Fill in the blanks:

(i) −19/5 lies between the integers __________ and __________.

Solution :

The decimal value of -19/5 is -3.8

In number line -3.8 lies between -4 and -3

−19/5 lies between the integers -4 and -3

(ii) The rational number that is represented by 0.44 is __________.

Solution :

In order to convert 0.44 as rational number, we have to multiply both numerator and denominator by 100.

0.44 x (100/100)  =  44/100

By reducing the fraction 44/100, we get

  =  11/25

(iii)  The standard form of + 58/(-78) is _________

Solution :

By simplifying 58/(-78), we get 

  =  -29/39

(iv)  The value of (-5/12) + (7/15)  =  

Solution :

L.C.M of (12, 15)  =  60

  =  [-5(5) + 7(4)]/60 

  =  (-25 + 28)/60

  =  3/60

  =  1/20

(v)  The value of 

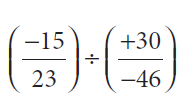
is 

Solution :

  =  (-15/23) x (-46/30)

By canceling 23 and 46, we get 2. In the same way by cancelling 15 and 30, we get 2.

  =  1

Question 2 :

Say True or False:

(i) 0 is the smallest rational number.

Solution :

Any number which is in the form of p / q , where p, q are integers and q ≠ 0 are called Rational numbers.

Q = { p / q : p , q ∊ Z , q ≠ 0 }

According to the definition there are infinite numbers less than ' 0 ' and greater than ' 0 '. Hence, the given statement is False.

(ii) There are an unlimited number of rational numbers between 0 and 1.

Solution :

Some numbers between 0 and 1 are 0.1, ............, 0.11, ...........

Hence the there are infinite numbers of rational numbers between 0 and 1. Hence the given statement is true.

(iii) The rational number which does not have a reciprocal is 0.

Solution :

The reciprocal of 0 is 1/0.

1/0  =  undefined

Hence 0, does not have reciprocal.

(iv) The only rational number which is its own reciprocal is –1.

Solution :

Reciprocal of -1 is 1/(-1)

  =  -1

Hence -1 is reciprocal of -1.

(v) The rational numbers that are equal to their additive inverses are 0 and–1.

The additive inverse of 0 is 0 and additive inverse of -1 is 1.

Hence the given statement is false.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.