PRACTICE QUESTIONS ON CONDITIONAL PROBABILITY

Question 1 :

Can two events be mutually exclusive and independent simultaneously?

Solution :

If two events A and B are mutually exclusive then 

P(AnB)  =  0    ----(1)

If two events A and B are independent then 

P(AnB)  =  P(A) ⋅ P(B)    ----(2)

(1)  =  (2)

P(A) ⋅ P(B)  =  0

Case 1 :

If either P(A) or P(B) be equal to 0, then the events will be mutually exclusive or independent.

Case 2 : 

If P(A) > 0 and P(B) > 0, then 

P(AnB)  =  P(A) P(B)  > 0 (Which is not equal to 0)

So, the events are independent not mutually exclusive.

Case 3 : 

If P(A) > 0 and P(B) = 0 or P(A) = 0 and P(B) > 0, then 

P(AnB)  =  P(A) P(B)  = 0 

So, the events are mutually not independent exclusive.

Hence, we may conclude that two events cannot be mutually exclusive and independent simultaneously.

Question 2 :

If A and B are two events such that P(A U B) = 0.7, P(A n B) = 0.2, and P(B) = 0.5, then show that A and B are independent.

Solution :

To show that event A and B are independent, we have to show that P(AnB)  =  P(A) ⋅ P(B)

P(AUB)  =  P(A) + P(B) - P(AnB)

0.7  =  P(A) + 0.5 - 0.2

0.7  =  P(A) + 0.3

0.7 - 0.3  =  P(A)

P(A)  =  0.4

P(AnB)  =  P(A) ⋅ P(B)

0.2  =  0.4 (0.5)

0.2  =  0.2

Hence the events A and B are independent.

Question 3 :

If A and B are two independent events such that P(A∪B) = 0.6, P(A) = 0.2, find P(B).

Solution :

Since A and B are independent events,

P(AUB) = P(A) x P(B)

P(A∪B) = 0.6, P(A) = 0.2

Since A and B are independent events, P(AnB)  =  0

P(AUB)  =  P(A) + P(B) - P(AnB)

P(AUB)  =  P(A) + P(B) - [P(A) x P(B)]

0.6 = 0.2 + P(B) ( 1 - P(A) )

0.4 = P(B) (1 - 0.2)

P(B) = 0.4/0.8

P(B) = 4/8

P(B) = 0.5

Question 4 :

If P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8, find P(A / B) and P(A∪B) .

Solution :

P(A/B)  =  P(AnB)/P(B)   ----(1)

P(B/A)  =  P(AnB)/P(A)

0.8  =  P(AnB)/0.5

0.8(0.5)  =  P(AnB)

P(AnB)  =  0.4

By applying the value of P(AnB) in (1), we get

P(A/B)  =  0.4 / (0.8)

P(A/B)   =  0.5

P(AUB)  =  P(A) + P(B) - P(AnB)

P(AUB)  =  0.5 + 0.8 - 0.4

P(AUB)  =  0.9

Question 5 :

If for two events A and B, P(A) = 3/4, P(B) = 2/5 and AUB = S (sample space), find the conditional probability P(A/B)

Solution :

P(A) = 3/4, P(B) = 2/5 and AUB = S

P(AUB)  =  P(A) + P(B) - P(AnB)

1  =   (3/4) + (2/5) - P(AnB)

1  =  (15 + 8)/20 - P(AnB)

  1  -  (23/20)  =  P(AnB)

  P(AnB)  =  3/20

P(A/B)  =  P(AnB)/P(B)

  =  (3/20) / (2/5)

  =  (3/20) ⋅ (5/2)

P(A/B)  =  3/8

Question 6 :

Consider the following table below.

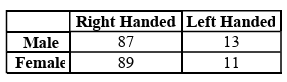
What is the probability that a randomly selected person is male given the person is left handed ?

a)  13/200     b)  13/50    c)  13/100    d)  13/24

Solution :

Number of male which are left handed = 13

Total number of left handed = 13 + 11

= 24

Probability that selected person is male given the person is left handed

= 13/24

Question 7 :

The table below shows the food preferences of sports fans whose favorite sport is football or baseball.

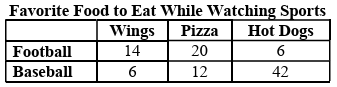
The probability that a fan prefers pizza given that the fan prefers football is

a) 1/2     b)  1/5   c)  5/8    d) 13/25

Solution :

Number of fans who prefer pizza = 20

Number of football fans = 14 + 20 + 6

= 40

Required probability = 20/40

= 1/2

So, option a is correct.

Question 8 :

The set of data in the table below shows the results of a survey on the number of messages that people of different ages text on their cell phones each month.

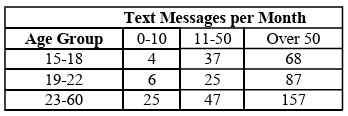
If a person from this survey is selected at random, what is the probability that the person texts over 50 messages per month given that the person is between the ages of 23 and 60?

a) 157/229     b) 157/312   c) 157/384    d) 157/456

Solution :

Total number of persons text messages over 50

= 68 + 87 + 157

= 312

Number of persons between the age of 23 to 60 and over 50 = 157

Required probability = 157/312

So, option b is correct.

Question 9 :

A survey about television-viewing preferences was given to randomly selected freshmen and seniors at Fairport High School. The results are shown in the table below.

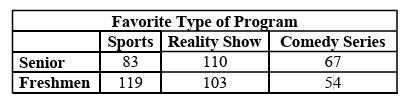
A student response is selected at random from the results. State the exact probability the student response is from a freshman, given the student prefers to watch reality shows on television.

Solution :

Numbero of persons whose favorite type is reality show

= 110 + 103

= 213

Number of freshman prefers reality show = 103

Required probability = 103/213 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.